CHAPTER I
INTRODUCTION
General:
The chief task of the structural engineer is the design of structures. The single most important characteristics of any structural member is its actual strength, which must be large enough to resist, with some margin to spare, all foreseeable loads that may act on it during the life of the structure without failure or other distress. It is logical, therefore, to proportion members, i.e., to select concrete dimensions and reinforcement, so that member strengths are adequate to resist forces resulting from certain hypothetical overload stages, significantly above loads expected actually to occur in service.
Background of study:
Concrete can be used in many different ways and often many different configurations are feasible. However, market prices, project requirements and site conditions affect the relative economics of each option. In assessing the structural cost of a multi-story building, it is evident that the bulk of the cost is often for the floor slab construction. Therefore, the overall economy of a structure may depend on the need for the efficiency and economy of the floor slab’ system. For a building, the choice of floor design is often determined by the need for long spans to provide floor space uninterrupted by cores and columns.Traditional concrete design for office/residential buildings have been associated with either beam and slab or flat slab floors typically with 18~22 ft spans. Occasionally, longer-span floors have designed using ribbed or waffle construction. In recent times changes in the requirements of end-users and in developer’s specifications have led to more open-plan floor spaces and larger floor-heights in two-way beam supported concrete floor systems. This has increased spans from 18~27 ft, even to 45 ft and more. The change in span length of the slab is directly related with the beam length and it affects the size of beams as well as columns and footings.To verify the competitiveness of concrete long-span floors based on cost analyses, this study was carried out as a partial fulfillment of the requirement for the degree of Bachelor of Science (B.Sc) in Civil Engineering.
Objectives and the study:
- To analysis and design two four storied residential building having same plinth area but different span length of the panels.
- To analyze, design and estimate slabs, floor beams, columns, grade beams and footings both slab systems.
- To compare between both slab systems based on required volumes of concrete & steel.
- To compare between both slab systems based on total costing.
Organization of the Thesis Works:
The thesis has been arranged in the following order also including references as well as appendices used for the study.
Chapter I: This includes the introduction, the objectives and the scope of the study.
Chapter II: Includes Literature Review.
Chapter III: Includes Design Codes & Specifications
Chapter IV: Includes the methodology of the study.
Chapter V: Provides structural design of the four storied Type-I building (short span floor system) by USD
Chapter VI: Provides structural design of the four storied Type-II building (longer span floor system) by USD
Chapter VII: Provides estimate and cost analyses for both structures
Chapter VIII: Provides comparative analyses between both structures and discussions
Chapter IX: Includes conclusions and suggestions for further study.
References
Appendices
Scopes/limitations of the study:
- The comparative study between the structures had been made based on low rise structural design concept. Selected structures were four storied (two-unit) residential building.
- All Slabs had been analyzed by ‘ACI moment co-efficient procedure’.
- Earthquake and wind loads were not considered in design.
- All slabs were considered as edge supported.
- For cost analyses, only frame structure (slabs, beams, columns, footings etc.) plus stair case were estimated.
- The cost analysis was done in accordance with the PWD schedule.
CHAPTER II
LITERETURE REVIEW
General:
Design of members and structures of reinforced concrete is a problem distinct from but closely related to analysis. Strictly speaking, it is almost impossible to exactly analyze a concrete structure, and to design exactly is no less difficult. Fortunately, we can make a few fundamental assumptions, which make the design of reinforced concrete, quite simple, if not easy. A problem unique to the design of reinforced concrete structures is the need to detail each member throughout. Steel structures, in general, require only the detailed design of connections. For concrete structures, we must determine not only the area of longitudinal and lateral reinforcement required in each member, but also the way to best arrange and connect the reinforcement to insure acceptable structural performance. This procedure can be made reasonably simple, if not easy. If we understand the basic concepts behind code provisions for design, we will be able to:
• approach the design in a more knowledgeable fashion, not like following a black box;
• understand and adapt the changes in code provisions better and faster.
Concrete structures: design components & types:
Generally, a concrete structure is made of a set of frames consisting of several vertical and horizontal members. That is why, it is known as “frame structure”. There are two types of frame structures:
a) Low Rise Structures: Total height is 40~60 ft above the ground level. Earthquake and wind loads are not considered during design of such structures. Generally, residential buildings are low-rise structures.
b) High Rise Structures: Total height is more than 60 ft above the ground level. Earthquake and wind loads are considered during design of such structures.
The whole frame structure is divided into three parts:
1) Superstructure: This is the portion which is above the ground level and consisted of the following design components:
a) Beams – All horizontal reinforced concrete member.
b) Slabs – Plain and flat reinforced concrete surfaces, which rest on beams. Two types: 1. Roof- Top slabs 2. Floors- all slabs except the top one.
c) Columns- all vertical reinforced concrete members on which beams rest.
2) Substructure: Portion of the structure, which is below the ground level. Basement floor, car parking etc. are constructed under the ground. Substructure also consists of beams, slabs and columns.
3) Foundation: This is the portion on which the total structure rest. Foundation of a structure may be footing or piling type.
Concrete structures: design basis:
The design of a concrete structure is based on the following design criteria:
1) Codes and specifications:
Structures must be designed and constructed according to the provisions of a code, which is a legal document containing requirements related to such things as structural safety, fire safety, plumbing, ventilation, and accessibility to the physically disabled. The American Concrete Institute (ACI) has published the ACI Building Code Requirements for Reinforced Concrete, which is usually referred to as the “ACI Code”. This is widely used as a legal set of rules by which r/c buildings are designed. If a structural designer correctly follows this set of rules, and the building, which the designer has designed, has structural problems or failures, then the designer cannot be blamed.
2) Loads
Loads that act on structures can be divided into three general categories:
Dead loads
Such loads are constant in magnitude and fixed in location throughout the lifetime of the structure. This is a fixed position gravity service load. This includes the weight of the actual structure itself, as well as anything non-movable that is permanently attached to the structure. Therefore, dead load includes the gravity load from floors, beams, ceilings, roofs, pipes (plumbing), ventilation ducts, and windows. It does not include furniture because they are movable. Dead loads can be accurately estimated by adding up the weights of the various parts of the structure.
Live loads
They are either fully or partially in place or not present at all, may also change in location. This is also a gravity load, but it is different from dead load because it varies in magnitude and location. Examples include people, furniture, cars, and stored goods. Live loads cannot be accurately estimated because the load is variable and unknown. For instance, before the building is built and the tenants have moved in, the designer does not know how many people and how much or what kind of furniture will be on any floor of the structure.
Environmental loads:
Loads from nature such as wind, earthquake, and snow loads, are known as Environmental Loads. They may change in magnitude as well as location.
All dead and live loads are considered as uniformly distributed loads acting on the structures.
Total uniformly distributed loads = Total dead loads + Total live loads
3) Materials
Concrete structures are made of two different types materials: Concrete and reinforcing steel
Concrete is a composite material composed of Portland cement, fine aggregate (sand), coarse aggregate (gravel/stone), and water. Quality of concrete is measured by its compressive strength, f’c.
Concrete has high strength when it is in compression. However, it is brittle and will crack when it is under tension. To increase the tension strength, steel reinforcing bars are added to the concrete while it is still wet. The concrete hardens around the reinforcing bars and the steel and concrete acts as one unit. To make the bond between the concrete and steel stronger, the reinforcing bars have small deformations, which interlock with the concrete.
The most common type of reinforcing steel is in the form of round bars, often called “rebars” available in diameters ranging from 3/8 to 1 3/8 in (Nos. 3 through 11) for ordinary applications such as in beams and in two heavy bar sizes of about 1 3/4 and 2 1/4 in (Nos. 14 and 18) such in columns.
Quality of the reinforcing steel is expressed by it yield strength, fy. Reinforcing bars with 40-ksi-yield stress, almost standard 20 years ago, have largely been replaced with 60-ksi-yield stress because they are more economical and their use tends to reduce congestion of steel in forms.
4) Safety
A structure must be safe against collapse; strength of the structure must be adequate for all loads that might act on it. If we could build buildings as designed, and if the loads and their internal effects can be predicted accurately, we do not have to worry about safety. But there are uncertainties in:
1. Actual loads;
2. Forces/loads might be distributed in a manner different from what we assumed;
3. The assumptions in analysis might not be exactly correct;
4. Actual behavior might be different from that assumed;
Finally, we would like to have the structure safe against brittle failure (gradual failure with ample warning permitting remedial measures is preferable to a sudden or brittle failure).
5) Design Methods
Two philosophies of design have long been prevalent. The working stress method, focusing on conditions at service load (that is, when the structure is being used), was the principal method used from the early 1900s until the early 1960s. Today, with few exceptions, the strength design method is used, focusing on conditions at loads greater than service loads when failure may be immanent. The strength design method is deemed conceptually more realistic to establish structural safety.
Review of the structural elements of a building:
Slab:
The slab provides a horizontal surface and is usually supported by columns, beams or walls. Slabs can be categorized into two main types: one-way slabs and two-way slabs. One-way slab is the most basic and common type of slab. One-way slabs are supported by two opposite sides and bending occurs in one direction only. Two-way slabs are supported on four sides and bending occurs in two directions. However, slabs supported by four sides may be assumed as one-way slab when the ratio of lengths to width of two perpendicular sides exceeds 2. Although while such slabs transfer their loading in four directions, nearly all load is transferred in the short direction.
Two-way slabs carry the load to two directions, and the bending moment in each direction is less than the bending moment of one-way slabs. Also two-way slabs have less deflection than one-way slabs. Compared to one-way slabs, Calculation of two-way slabs is more complex. Methods for two-way slab design include Direct Design Method (DDM), Equivalent frame method (EFM), Finite element approach, and Yield line theory. However, the ACI Code specifies two simplified methods, DDM and EFM.
Types of Slabs
• One-way slab
1. One-way beam and slab / One-way flat slab:
These slabs are supported on two opposite sides and all bending moment and deflections are resisted in the short direction. A slab supported on four sides with length to width ratio greater than two, should be designed as one-way slab.
2. One-way joist floor system:
This type of slab, also called ribbed slab, is supported by reinforced concrete ribs or joists. The ribs are usually tapered and uniformly spaced and supported on girders that rest on columns.
• Two-way slab
1. Two-way Edge Supported slab:
If the slab is supported by beams on all four sides (as shown in Figure 2.1), the loads are transferred to all four beams, assuming rebar in both directions.
n Advantages:
- Increased gravity and lateral load resistance
- Increased torsional resistance
- Decreased slab edge displacements
- Economical for longer spans and high loads
n Disadvantages:
- Presence of beams may require greater storey height
- Requires a regular column layout
- Grid of downstand beams deters fast formwork recycling
- Flexibility of partition location and horizontal service distribution may be compromised.
n Typical Applications:
- Economical for more heavily loaded spans from 25 to 35 ft
- Generally used for retail developments, warehouses, stores, etc
2. Two-way flat plate slab:
A flat plate slab (as shown in Figure 2.2) usually does not have beams or girders and is supported directly on columns. All loads are transferred to the supporting column, with punching shear resisted by slab itself.
n Advantages:
- Simple and fast formwork and construction
- Absence of beams allows lower storey heights
- Flexibility of partition location and horizontal service distribution
- Architectural finish can be applied directly to the underside of slab
n Disadvantages:
- higher cost and higher deflections
- Holes can prove difficult, especially large holes near columns
- Shear provision around columns may need to be resolved using larger columns, column heads, drop panels or proprietary systems
n Typical Applications:
- Flat slabs are popular for office buildings, hospitals, hotels, blocks of flats, etc.
- For LL=50 psf, 25’ – 30’ spans
- For LL=100 psf, 20’ – 30’ spans
3. Two-way Flat slab:
Flat plate with drop panels, shear capitals, and/or column capitals (as shown in Figure 2.3).
Advantages:
- Reduced slab displacements
- Increased slab shear resistance
- Relatively flat ceilings (reduced finishing costs)
- Low story heights due to shallow floors
Disadvantages:
- Need more formwork for capital and panels
Typical Applications:
- Medium spans with moderate to heavy loading
- Popular for office buildings, hospitals, hotels, etc.
- For LL=50 psf, 30’ – 35’ spans
- For LL=100 psf, 25’ – 35’ spans
Beam:
Beams can be described as members that are mainly subjected to flexure and it is essential to focus on the analysis of bending moment, shear, and deflection. When the bending moment acts on the beam, bending strain is produced. The resisting moment is developed by internal stresses. Under positive moment, compressive strains are produced in the top of beam and tensile strains in the bottom. Concrete is a poor material for tensile strength and it is not suitable for flexure member by itself. The tension side of the beam would fail before compression side failure when beam is subjected a bending moment without the reinforcement. For this reason, steel reinforcement is placed on the tension side. The steel reinforcement resists all tensile bending stress because tensile strength of concrete is zero when cracks develop. In the Ultimate Strength Design (USD), a rectangular stress block is assumed. The design of beam is initiated by the calculation of moment strengths controlled by concrete and steel
Types of beam:
Most common shapes of concrete beams: single reinforced rectangular beams, doubly reinforced rectangular beams, T-shape beams; spandrel. In cast–in-place construction, the single reinforced rectangular beam is uncommon. The T-shape and L-shape beams are typical types of beam because the beams are built monolithically with the slab. When slab and beams are poured together, the slab on the beam serves as the flange of a T-beam and the supporting beam below slab is the stem or web. For positive applied bending moment, the bottom of section produces the tension and the slab acts as compression flange. But negative bending on a rectangular beam puts the stem in compression and the flange is ineffective in tension. Joists consist of spaced ribs and a top flange.
Column:
Columns support primarily axial load but usually also some bending moments. The combination of axial load and bending moment defines the characteristic of column and calculation method. A column subjected to large axial force and minor moment is design mainly for axial load and the moment has little effect. A column subjected to significant bending moment is designed for the combined effect. The ACI Code assumes a minimal bending moment in its design procedure, although the column is subjected to compression force only. Compression force may cause lateral bursting because of the low-tension stress resistance. To resist shear, ties or spirals are used as column reinforcement to confine vertical bars. The complexity and many variables make hand calculations tedious which makes the computer-aided design very useful.
Types of columns:
Reinforced concrete columns are categorized into five main types; rectangular tied column, rectangular spiral column, round tied column, round spiral column, and columns of other geometry (Hexagonal, L-shaped, T-Shaped, etc).
Tied columns have horizontal ties to enclose and hold in place longitudinal bars. Ties are commonly No. 3 or No.4 steel bars. Tie spacing should be calculated with ACI Code. Spiral columns have reinforced longitudinal bars that are enclosed by continuous steel spiral. The spiral is made up of either large diameter steel wire or steel rod and formed in the shape of helix. The spiral columns are slightly stronger than tied columns.
Footing:
The foundation of a building is the part of a structure that transmits the load to ground to support the superstructure and it is usually the last element of a building to pass the load into soil, rock or piles. The primary purpose of the footing is to spread the loads into supporting materials so the footing has to be designed not to be exceeded the load capacity of the soil or foundation bed. The footing compresses the soil and causes settlement. The amount of settlement depends on many factors.
Excessive and differential settlement can damage structural and nonstructural elements. Therefore, it is important to avoid or reduce differential settlement. To reduce differential settlement, it is necessary to transmit load of the structure uniformly. Usually footings support vertical loads that should be applied concentrically for avoid unequal settlement. Also the depth of footings is an important factor to decide the capacity of footings. Footings must be deep enough to reach the required soil capacity.
Types of footings:
The most common types of footing are strip footings under walls and single footings under columns.
Common footings can be categorized as follow:
1. Individual column footing:
This footing is also called isolated or single footing. It can be square, rectangular or circular of uniform thickness, stepped, or sloped top. This is one of the most economical types of footing. The most common type of individual column footing is square of rectangular with uniform thickness.
2. Wall footing:
Wall footings support structural or nonstructural walls. This footing has limited width and a continuous length under the wall.
3. Combined footing:
They usually support two or three columns not in a row and may be either rectangular or trapezoidal in shape depending on column. If a strap joins two isolated footings, the footing is called a cantilever footing.
4. Mat foundation:
Mats are large continuous footings, usually placed under the entire building area to support all columns and walls. Mats are used when the soil-bearing capacity is low, column loads are heavy, single footings cannot be used, piles are not used, or differential settlement must be reduced through the entire footing system.
CHAPTER III
DESIGN SPECIFICATIONS & PROCEDURES
Introduction
Structures must be designed and constructed according to the provisions of a code, which is a legal document containing requirements related to such things as structural safety, fire safety, plumbing, ventilation, and accessibility to the physically disabled. Many countries have building codes to define material properties, quality controls, minimum size, etc for safety constructions.
Design code & specifications:
The American Concrete Institute (ACI) is leading the development of concrete technology. The ACI has published many references and journals. Building Code Requirement for Structural Concrete (ACI318 Code) is a widely recognized reinforced concrete design and construction guide. Although the ACI Code dose not has official power of enforcement, it is generally adapted as authorized code by jurisdictions not only in United States but also many countries.
The ACI318 Code provides the design and construction guide of reinforced concrete. ACI has been providing new codes depending on the change of design methods and strength requirement. In our country, we have similar design standard which is “Bangladesh National Building Code (BNBC). This confronts with the ACI specifications.
Two major calculating methods of reinforced concrete have been used from early 1900’s to current. The first method is called Working Stress Design (WSD) and the second is Ultimate Strength Design (USD).
Ultimate Strength Design (USD) Method:
The Ultimate Strength Design method, also called Strength Design Method (SDM), is based on the ultimate strength, when the design member would fail. The USD method provides safety not by allowable stresses as for the ASD method but by factored loads, nominal strength and strength reduction factors θ, both defined by the ACI code.
Select concrete dimensions and reinforcements so that the member strength are adequate to resist forces resulting from certain hypothetical overload stages, significantly above loads expected actually to occur in service. Based on strength design the nominal strength of a member must be calculated on the basis of inelastic behavior of material. In other words, both reinforcing steel and concrete behave inelastically at ultimate strength condition.
The strength design method may be expressed by the following,
“Strength provided ≥ Strength required to carry factored loads”
Where the “strength provided” such as moment strength is computed in accordance with rules and assumptions of behavior prescribed by a building code, and the “strength required” is that obtained by performing a structural analysis using the factored loads.
Combination of loads & ACI load factors:
The required strength U is expressed in terms of factored loads, or related internal moments and forces. Factored loads are the loads specified in the general building code multiplied by appropriate factors. The factor assigned is influenced by the degree of accuracy to which the load effect can be determined and the variation, which might be expected in the load during the lifetime of the structure. Dead loads are assigned a lower load factored than live load because they can be determined more accurately. Load factors also account for variability in the structural analysis used to compute moments and shears. Since the factored load is a failure load greater than the actual working loads, the load factors are usually greater than unity.
The code gives load factors for specific combinations of loads. In assigning factors to combinations of loading, some consideration is given to the probability of simultaneous occurrence. While most of the usual combinations of loadings are included, the designer should not assume that all cases are covered.
Load combinations:
U = 1.4D only for dead loads
U = 1.2D + 1.6L for dead plus live loads combined.
Design considerations & ACI/BNBC code provisions
Slab
Minimum slab thickness
Minimum thickness h of non pre stressed one-way slabs
- Simply supported, h =
- One end continuous, h =
- Both ends continuous, h=
- Cantilever, h = ; where, L = clear span
The slab thickness for a two ways slab (edge supported by DDM) must not be less than
inch (for)
inch (for )
Where, = Clear span in long direction, in.
= Average value of for all beams on edges of a panel.
Ratio of clear span in long direction to clear span in short direction.
And
Ib , Is = Moment of Inertia of beam and slab
To limit deflections, the ACI code provides that the minimum thickness of a two way slab shall be 3.5 inch or the ‘panel perimeter divided by 180’, whichever is larger.
Provision for reinforcement arrangement:
Deformed reinforcement shall be provided in accordance with the following:
# Minimum Main reinforcement: The ACI code requires the area provided must not be less then
# According to ACI code minimum ratios of temperature and shrinkage reinforcement in slabs based on gross concrete area.
- Slabs where ‘Grade 40’ or ‘Grade 50’ deformed bars are used = 0.0020
- Slabs where ‘Grade 60’ deformed bars or welded wire fabric (smooth or deformed) are used = 0.0018
- Slabs where reinforcement with yield strength exceeding 60,000 psi. measured at yield strain of 0.35 percent is used
For arrangement of steel the BNBC code provides the following specifications
- Surface not exposed to weather, clear covering
- Surface exposed to weather, clear covering
- The minimum clear spacing between parallel bars in a layer shall be equal to one bar diameter or 1 inch
- Placed directly above those in the bottom layer with clear distance between layers 1 inch.
- In one-way slabs the maximum bar spacing shall be 3h 18 inch.
- For two-way slabs, maximum spacing of bars shall be 2h 18 inch.
- For temperature steel only, maximum spacing shall be 5h 18 inch.
Load calculation
Total load, Wt = 1.6 x Live load + 1.2 x (Self weight of slab + Load due to floor finish etc)
Effective depth check
Where, = Maximum ultimate moment. = Strength reduction factor.
= Maximum Steel ratio.
Reinforcement calculation and arrangement
Where checking the assumed depth by,
Spacing =
Where, = Area of using reinforcement.
Beam
Reinforcement arrangement in a beam based on ACI code:
ACI Code has specified many rules and restrictions on placement of the tensile reinforcements in a beam. Standard bend points for bars in approximately equal spans with uniformly distributed loads are shown in Figure 3.1. If Exterior support is a simply supported (such as brick wall), bend point for the main steel will be L1/7 from the ext. support face instead of L1/4, where L1 = clear span.
# Stirrups: They are used to hold the main (tensile) steel in their places and sometimes; they resist shear force in the beam. Generally, #3 and #4 bars are used as stirrups but in the bridge girders, #5 bar is used. Stirrups should be carried as close as possible to the compression and tension faces of a beam and special attention must be given to proper anchorage. Stirrups normally are types-open & closed and are provided with 90° or a 135° hooks at their upper end and at their lower end, are bent 90° to pass around the longitudinal reinforcement. Details of stirrups are shown in Figure 3.2.
# Tensile bars: They are the main bars in a beam and placed in tension side. The strength of a beam is directly related to this steel and if they fail, the beam collapses as a whole. The most common type of tensile reinforcement is available in diameters ranging from 3/8 to 1 3/8 in (Nos. 3 through 11) for ordinary applications such as in beams and in two heavy bar sizes of about 1 3/4 and 2 1/4 in (Nos. 14 and 18) such in columns. The total numbers required for design is denoted by “n” and the diameter of a bar is expressed by “db”.
# Hooked bars: In event that the desired tensile stress in a bar cannot be developed by bond alone, it is necessary to provide special anchorage at the ends of the bar, usually by means of a 90° or a 180° hook. They are known as hook bars. Generally, such bars are bent or straight types and are provided at the end of the tensile bars and stirrups and tie bars. The dimensions and bend radii for such hooks have been standardized in ACI Code as follows:
For tensile bars:
- A 180° bend plus an extension of at least 4 bar diameters, but not less than 2.5 in. at the free end of the bar, or
- A 90° bend plus an extension of at least 12 bar diameters at the free end of the bar.
For tie bars:
- For #5 bars and smaller, a 90° bend plus an extension of at least 6 bar diameters at the free end of the bar, or
- For #6, #7 and #8 bars, a 90° bend plus an extension of at least 12 bar diameters at the free end of the bar, or
For stirrups:
For #8 bars and smaller, a 135° bend plus an extension of at least 6 bar diameters at the free end of the bar.
Bar placement is described with the help of the cross-section of the beam in Figure 3.3 and Figure 3.4.
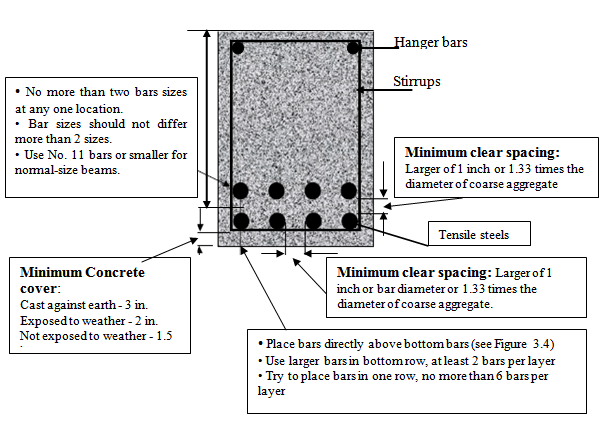
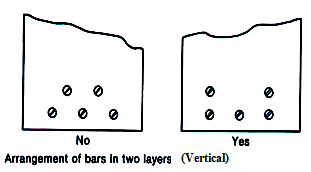
# Minimum clear spacing between bars: Minimum spacing (horizontally Sh and vertically Sv, face-to-face) between bars is required to ensure proper placement of concrete around them. Air pockets below the steel are to be avoided and full surface contact between the bars and the concrete is desirable to optimize bond strength. The horizontal spacing is directly related to the beam width, b.
# Effective Depth: The distance between the upper face of the beam and the centroid of the tensile steel. It is denoted by “d”.
d = Total depth – concrete cover – stirrup diameter – half of the main bar diameter
= Total depth – clear cover
Considering this,
d = h – 2.5 for single layer of steel
= h – 3.5 inch for double layers of steels
= h – 4.5 inch for three layers of steels
# Hanger bars: In simple spans, or in the positive bending region of continuous spans, where no top bars are required for flexure, stirrups support bars should be used. Such bars are known as hanger bars. These are usually about the same diameter as the stirrups themselves, and they not only provide improved anchorage of the hooks but also facilitate fabrication of the reinforcement case, holding the stirrups in position during pouring of the concrete.
# Minimum Concrete Cover: It is required for the following reasons:
[a] Bonds reinforcement to concrete [b] Protect reinforcement against corrosion
[c] Protect reinforcement from fire (over heating causes strength loss)
Development of flexural reinforcement
According to BNBC code
- Reinforcement shall extend beyond the point at which it is no longer required to resist flexure for a distance not less than d nor less than 12, except at supports of simple spans and at free end of cantilevers.
- At least one-third of the total tension reinforcement provided for negative moment at the support shall be extended beyond the extreme position of the point of inflection a distance not less than ‘one-sixteenth the clear span’, or 12, whichever is greater
- At least one-third of the positive moment reinforcement in simple members and one-fourth of the positive moment reinforcement in continuous members shall extend alone the same face of member into the support. In beams, such reinforcement shall extend into the support at least 6 inch.
Beam design:
Depth check:
Steel ratiovaries (ACI) from an upper limit of to a lower limit of . But code specifies a check for deflections if
where for flexural member
where,
Design of beam for shear
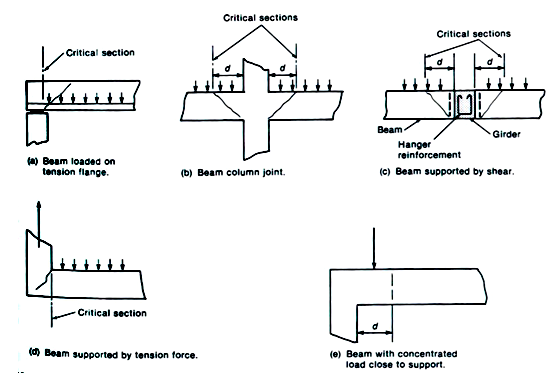
Due to local compressive forces from the support, diagonal tension failure cannot occur very near to support, as shown in Figure 3.5 below:
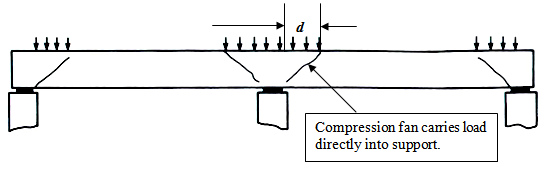
For this reason, ACI Code defines,
a) For beams, monolithically cast with the support (i.e. direct support such as column), the critical section is at a distance “d” from the support face, as shown in Figure 3.6,
where, “d” = effective depth of beam. Also, for simply supported beam, this critical section is at a distance “d” from the support centerline.
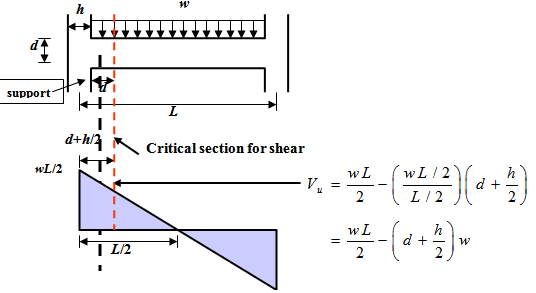

b) If support is not a direct support (beam etc), then critical section should be taken at the face of support.
A typical example is shown in the below Figure 3.7. The load of beam 1 is transmitted to beam 2 mainly through the last inclined concrete strut. Beam 1 has an indirect support and critical section is at the face of indirect support.
If load is applied to beam on tensile face, critical section for shear is at the face of support. If beam is hanging to another member and tension occurs in that member, than support of beam is indirect support.
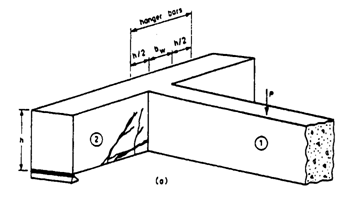
Critical sections for different types of structures are shown in Figure 3.8 below:
Design of shear reinforcement
Shear strength provided by concrete
Simply
Maximum allowable shear
Design for web:
When , web must be provided
For vertical stirrups
Spacing of shear reinforcement:
If then (i) Or (ii) Or (iii)
should be the smaller one of above.
If , then shall be reduced by one-half of (i), (ii), (iii)
For doubly reinforced beam stirrups diameter and spaced not farther apart than. Ties should be used throughout the distance in which the compression reinforcement is required.
Column:
Specifications
(i) Limiting dimension
- Tide column least dimension
- Spiral column diameter
- Provided that gross area should not be less than 96 sq.inch
(ii) The reinforcement ratio of the longitudinal steel shall be not less then 0.01 nor more than 0.08 (Usually less than 0.04).
(iii) Size of longitudinal bars used #5
- For tide column at least 4 bars.
- For spiral column at least 6 bars.
(iv) Arrangement of lateral ties
- All bars shall be enclosed by lateral ties, at least #3 in size for longitudinal bars for and #4 in size for longitudinal bars for #11, #14 and #18
- Vertical spacing of ties shall not exceed ‘16 longitudinal bar diameters’ or ‘48 tie diameters’, or the ‘least dimension of the compression members’.
- Ties shall be arranged such that every corner and alternate longitudinal bar shall have lateral support provided by the corner of a tie with an included angle not more than 135 deg. No vertical bar shall be farther than 6 inch clear on each side along the tie from such a laterally supported bar. Where longitudinal bars are located around the perimeter of a circle, a complete circular tie is allowed.
- The lowest tie in any storey shall be placed within one-half the required tie spacing from the top most horizontal reinforcement in the slab or footing below. The uppermost tie in any storey shall be within one-half the required tie spacing from the lowest horizontal reinforcement in the slab or drop panel above.
(v) Arrangement of lateral spirals
- Spirals shall consist of evenly spaced continuous bar or wire of such size and so assembled as to permit handling and placing without distortion from designed dimensions.
- Size of spirals shall not be less than #3 in size for cast-in-place construction.
- The minimum and maximum clear spacing between spirals shall be 1 inch and 3 inch respectively.
- Anchorage of spiral reinforcement shall be provided by 1.5 extra turns of spiral bar or wire at each end of a spiral unit.
Column design.
1. For tide column:
(Where)
( is selected)
2. For spiral column:
(Where)
( is selected)
Spiral reinforcement design
(Where and spiral pitch,
CHAPTER IV
METHODOLOGY OF THE STUDY
General:
This chapter gives the outlines of the procedures that were followed to complete this study. Few steps were considered, many references (Chapter II) were gone through and ACI/BNBC Building Design Codes/Specifications (Chapter III) were followed to get perfect result so that the objectives of this study can be fulfilled.
Research procedures:
Step-I: Selection and planning of the structure
Two four storied residential (two unit) frame structure (edge supported) having same floor plan has been selected-one has regular floor spans and other has longer spans. Their typical floor plan, panel plan, floor beam layout plan, column and footing layout plan and grade beam layout plan are drawn as given in Appendices VI ~ XV.
Step-II: Selection of the material properties & loadings
As per discussions made in Chapter II and based on design code/specifications of ACI/BNBC, material properties (compressive strength of concrete, yield stress of steel, unit weight of concrete, soil, brick etc.) and loadings (standard live load, floor finish, partition wall loads etc.) are selected. No wind and earthquake loads are considered.
Step-III: Design of the structure
The both structures are designed by ultimate strength design (USD) following low rise design concept. Chapter V & VI provides detailed structural design of the structure having edge supported slab with regular span (Type-I) and other with longer span (Type-II) respectively.
Step-IV: Estimation & cost analysis
After completion of the design, the volume of concrete and steel are estimated and finally, their costing are determined for both types of structures. Chapter VII presents this information.
Step-V: Comparison between both type structures
All results are summarized in several tabular forms as presented in Chapter VIII and in order to make comparative analyses, following criteria are considered:
- Sectional properties
- Volume of concrete
- Volume of steel
- Costings.
Step-VI: Conclusions & Recommendations
Based on comparative analyses and discussions, few concluding remarks are drawn. To carry out further study on this topic, recommendations are proposed in the Chapter IX.
Design data and specifications considered in this study:
The whole study was carried out based on few considerations and specifications which are summarized in Table 4.1 below.
Table 4.1: Summary of the design considerations and specification of the study
|
Items |
Description |
|
Design method |
Ultimate Strength Design (USD) |
|
Design procedure |
|
|
Design Code |
For design purposes:
- American Concrete Institute (ACI) Building design code, 2005
- BangladeshNationalBuilding Code (BNBC), 1993
For estimation and costing:
- Schedule of Rate for Civil Works, 12th edition, Public Works Department (PWD), 2008
Types of structures
Type-1: Edge supported structure having regular floor spans
Type-II: Edge supported structure having longer floor spans compared to the Type-I.
Building system
- Frame structure
- Low rise
- Residential (4 storied double unit)
Table 4.1: Summary of the design considerations and specification of the study (contd…)
Design considerations
- Estimation and cost analyses are done only for concrete and steel works of the frame structures (slab, floor beams, columns, grade beams and footings plus stair case).
- Brick works, shuttering works, electrifications and wiring works, sanitary works, plastering & finishing works, earth cutting & filling works and all fitting & fixing works, all types of labor costing etc are not considered in estimation and cost analysis
- Underground reservoir tank, overhead water tank, lintels over doors & windows, sunshade, porch etc are not considered in estimation and cost analyses.
Material properties
- Reinforcing bars : fy = 40 ksi for slab and 60 ksi for other cases
- Concrete compressive strength, f’c = 3,000 psi
- Normal density concrete having wc = 150 pcf
- Unit weight of soil, ws = 100 pcf
- Unit weight of brick, wb = 120 pcf
- Bearing capacity of soil, qa = 4.5 ksf
- Steel ratio for column, ρg = 2%
- Ratio of the ingredients = 1.0:1.5:3.0
- FM of normal sand = 2.5
Loadings
- Floor plus ceiling finish and partition walls = 30 psf
- Live load = 40 psf for slab and 100 psf for stair
- No earthquake and wind load are considered
Members’ Sectional properties
- Slab type = Two-way and one-way
- Beam type = Singly rectangular
- Column type = Tied
- Footing type = Square, rectangular and combined
- Grade beam position = 5 ft. from footing base level
- Thickness of all walls = 5 inch
CHAPTER V
STRUCTURAL DESIGN OF TYPE-I BUILDING
Introduction:
In this chapter, the four storied building is analyzed and designed by ultimate strength design (USD) method as per discussions made in Chapter III and references provided by Winter and Nilson (1997 & 2003). For space limitations, one set of design example is presented here in detail from each component of the building such as slab, floor beam, column, grade beam and footing. The cross-sectional dimensions along with reinforcement arrangement of the rest are shown in a tabular form.
Analysis and design of building components
Design of slab
All slab panels are analyzed and designed by following the ‘ACI Moment Coefficient procedure’ (Appendix I). Typical floor plan and panel plan are given in Appendix VI and Appendix VIII respectively. Analysis and design of the largest panel group (S-1) are presented below.
Design data:
Design procedure – ACI moment co-efficient
Materials:
= 40 ksi
= 3 ksi
= 150 pcf
= 120 pcf
Loadings:
F.F + partition wall = 30 psf
L.L = 40 psf
Slab panel S -1
Panel size = 14’x 22’
Beam width = 12″
Clear span size =13’x 21’
Panel ratio,
Panel type = Two-way slab (case – 4)
1) Load calculation:
Slab thickness
Self weight of slab
Floor finish +P-wall = 30 psf.
Live load = 40 psf.
Factored load = 1.2 WDL + 1.6 WLL
= 1.20×92.5+1.6×40
= 175 psf
ll) Moment calculation:
Support moment
Mid span moment
lll) Check for d :
Maximum moment = 2561.19 lb-ft.
lV) Reinforcement calculation:
Short direction (mid span)
< 200 psi
Use # 3 bar which area = 0.11
Spacing≈ > 2h = 2 x 5 =
Use # 3 @ alternate cranked bars.
Short direction (at support)
> 2h = 10’’
Crank to crank spacing
So we provide 1#3 extra top in between ckd. bars.
Long direction (mid span)
+MB = 689.28 lb – ft
Spacing > 2h = 2 x 5 = 10” c/c
Use # 3 @ alternate cranked bars.
Long direction (at support)
-MB = 1034.145 lb – ft
Spacing
Spacing > 2h = 2 x 5 = 10” c/c
Crank to crank spacing
So we provide 1#3 extra top between ckd. bars.
A detail of slab reinforcement arrangement of all panels (S-1 ~ S-5) is given in Table 5.1 and Figure 5.1.
Bar arrangement, cut-off and bent up, bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Table 5.1: Details of slab reinforcement arrangement of all panels (S-1 ~ S-5)
|
Panel |
Length (feet) |
Moment (pound-feet) |
Area of steel (inch sq./ft) |
Spacing (inch c/c) |
||||||||||
|
LA |
LB |
Negative |
Positive |
Negative |
Positive |
Negative (Extra top) |
Positive (Main bar) |
|||||||
|
LA |
LB |
LA |
LB |
LA |
LB |
LA |
LB |
LA |
LB |
LA |
LB |
|||
|
S-1 |
13 |
21 |
2561.19 |
1034.14 |
1652.68 |
689.28 |
0.144 |
0.24 |
0.096 |
0.096 |
#3 @ 10” |
#3 @ 10” |
#3 @ 10” |
#3 @10” |
|
S-2 |
13 |
21 |
2478.38 |
555.66 |
1258.51 |
544.72 |
0.144 |
0.24 |
0.096 |
0.096 |
#3 @ 10” |
#3 @ 10” |
#3 @ 10” |
#3 @10” |
|
S-3 |
13 |
18 |
2129.4 |
1587.6 |
1274.43 |
965.24 |
0.122 |
0.096 |
0.096 |
0.096 |
#3 @ 10” |
#3 @ 10” |
#3 @ 10” |
#3 @10” |
|
S-4 |
13 |
18 |
2235.87 |
929.88 |
1014 |
673.98 |
0.127 |
0.096 |
0.096 |
0.096 |
#3 @ 10” |
#3 @ 10” |
#3 @ 10” |
#3 @10” |
|
S-5 |
7 |
12 |
711.72 |
393.12 |
487.37 |
164.59 |
0.096 |
0.096 |
0.096 |
0.096 |
#3 @ 10” |
#3 @ 10” |
#3 @ 10” |
#3 @10” |
LA – Short direction
LB – Long direction
Figure 5.1: Details o
Design of floor beam:
All floor beams are analyzed and designed by following the ‘ACI Moment Coefficient procedure’ (Appendices I & XVII). Typical lay-out plan of all floor beams is given in Appendix-X. Analysis and design of one of the heavily loaded beam group (F. B – 2) is presented below.
Design data:
Design procedure = ACI moment co-efficient
Materials:
= 60 ksi
= 3 ksi
= 150 pcf
= 120 pcf
Main wall thickness = 5”
Floor beam F.B-2
Beam size = 12”x18”
Effective depth, d = 18”- 2.5” = 15.5”
l) Load calculation:
Self weight of beam F.B-2 =
All main wall weight
Load coming from slabs
S-1 & S-2 DL = 92.5x 14x.897 = 1161.615 lb / ft
Total DL = 1161.615+225+425 = 1812 lb / ft
LL = 40x14x.897 = 502.32 lb / ft
Factored load F.B-2 = 1.2DL+1.6LL = 1.2×1.81+1.6x0.502 = 2.975 k / ft
ll) Moment calculation & d check:
– ve moment at Ext. support =
+ ve moment at mid span =
– ve moment at Int. support =
= 160 k-ft
lll) Reinforcement calculation :
Mid span steel:
Use 1#7 Extra top in between 2#7 straight bars.
Steel for Int. support:
Use 2#8 Extra top in between 2#7 hanger bars.
lV) Stirrup design:
Details of sectional dimensions and reinforcement arrangement of all floor beams (FB -1 ~ FB-5) are given in Table 5.2 and Figure 5.2 & Figure 5.3.
Bar arrangement, cut-off and bent up, bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Table 5.2: Details of sectional dimensions and reinforcement arrangement of all floor beams (FB -1 ~ FB-5)
|
Floor beam group |
Floor beam size |
Moment (kip-ft) |
Area of steel req. (sq. inch) |
Quantity of bars |
Stirrups (spacing, inch c/c) |
|||||
|
At Ext. M-ve |
At Mid M+ve |
At Int. M-ve |
At Ext. As-ve |
At mid As+ve |
At Int. M-ve |
Main bars |
Extra top |
Use 2 Legs “U” #3 bar |
||
|
F.B-1 & 3 |
12” x 16” |
54.75 |
62.57 |
97.34 |
0.97 |
1.20 |
1.84 |
At Ext. suppt: 2- #6 |
1- #5 |
@ 6.5”c/c |
|
At mid span : 2- #6 |
1- #6 |
@ 6.5”c/c |
||||||||
|
At Int. suppt.: 2- #6 |
2- #7 |
@ 6.5”c/c |
||||||||
|
F.B-2 |
12” x 18” |
90.00 |
102.85 |
160.00 |
1.42 |
1.64 |
2.78 |
At Ext. suppt: 2- #7 |
1- #5 |
@ 5.5”c/c |
|
At mid span : 2- #7 |
1- #7 |
@ 5.5”c/c |
||||||||
|
At Int. suppt.: 2- #7 |
2- #8 |
@ 5.5”c/c |
||||||||
|
F.B-4 |
12” x 12” |
13.59 |
15.96 |
24.17 |
0.32 |
0.47 |
0.63 |
At Ext. suppt: 2- #5 |
– |
@ 5.5”c/c |
|
At mid span : 2- #5 |
– |
@ 5.5”c/c |
||||||||
|
At Int. suppt.: 2- #5 |
1- #5 |
@ 5.5”c/c |
||||||||
|
F.B-5 |
12” x 12” |
16.78 |
19.60 |
30.48 |
0.41 |
0.49 |
0.76 |
At Ext. suppt: 2- #5 |
– |
@ 5.5”c/c |
|
At mid span : 2- #5 |
– |
@ 5.5”c/c |
||||||||
|
At Int. suppt.: 2- #5 |
1- #5 |
@ 5.5”c/c |
||||||||
Design of column:
Typical lay-out plan of all columns is given in Appendix XII. Analysis and design of one of the heavily loaded column group (C – 3) is presented below.
Design data:
Column height =
Column type = Tied
Clear cover =
Materials:
= 60 ksi
= 3 ksi
= 150 pcf
Column C-3 (Ground column Interior):
Assume Column size =
l) Load calculation:
Load from F.B-2 = kip
Load from F.B-2 = kip
Load from F.B-5 = kip
Self weight of column == 1.58 kip
Factored load = 1.2×1.58+32.45+26.55+19.6= 80.5 kip
Total column load for 4-story = 4x 80.5 =322 kip
ll) Check for size:
PU = 322 kip (Story-1)
III) Calculation of steel
Details of sectional dimensions and reinforcement arrangement of all columns (C -1 ~ C -3) are given in Table 5.3 and Figure 5.4.
Bar arrangement, cut-off and bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Table 5.3: Details of sectional dimensions and reinforcement arrangement of all columns (C -1 ~ C -3)
|
Column group |
Number of column |
Column size |
Column load |
Area of steel req. (sq. inch) |
Quantity of bars |
Tie bars spacing |
|
Pu (kip) |
Ast |
Main bars |
Use #3 bars |
|||
|
C-1 |
04 |
115.72 |
0 .84 |
4-#5 |
10”c/c |
|
|
C-2 |
10 |
189.40 |
0.31 |
4-#5 |
10”c/c |
|
|
C-3 |
04 |
322 |
2.55 |
8-#5 |
12”c/c |
Design of grade beam:
All grade beams are analyzed and designed by following the ‘ACI Moment Coefficient procedure’ (Appendices I & XVII). Typical lay-out plan of all grade beams is given in Appendix XIV. Analysis and design of one of the heavily loaded beam group (GB-2) is presented below.
Design data:
Design procedure = ACI moment co-efficient
Materials:
= 60 ksi
= 3 ksi
= 150 pcf
= 120 pcf
Thickness of wall on GB = 5”
Clear cover = 3”
Grade beam GB-2:
Size =10” x 12”
Effective depth d =12-3.00 = 9 inch
I) Load calculation:
Self weight of beam GB-2 =
All main wall weight
Total DL = 125+425 = 550 lb / ft
Factored load GB-2 = 1.2DL = 1.2×0.55 = 0.66 k / ft
ll) Moment calculation & d check:
– Ve moment at Int. support =
+ Ve moment at mid span =
– Ve moment at Ext. support =
Now,
= 35.49 k-ft
lll) Reinforcement calculation :
Mid span steel:
Steel for Int. support:
Use 1#6 extra top in between 2#5 hanger bars
lV) Stirrup design:
Details of sectional dimensions and reinforcement arrangement of all grade beams (GB -1 ~ GB-2) are given in Table 5.4 and Figure 5.5.
Bar arrangement, cut-off and bent up, bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Table 5.4: Details of sectional dimensions and reinforcement arrangement of all grade beams (GB -1 ~ GB-2)
|
Grade beam group |
Grade beam size |
Moment (kip-ft) |
Area of steel req. (sq.inch) |
Quantity of bars |
Stirrups (spacing, inch c/c) |
|||||
|
At Ext. M-ve |
At Mid M+ve |
At Int. M-ve |
At Ext. As-ve |
At mid As+ve |
At Int. M-ve |
Main bars |
Extra top |
Use 2Legs “U” #3 bar |
||
|
G.B-1 |
10”x12” |
19.96 |
22.82 |
35.49 |
0.49 |
0.57 |
0.92 |
At Ext. suppt: 2-#5 |
– |
@ 3.5”c/c |
|
At mid span : 2-#5 |
– |
@ 3.5”c/c |
||||||||
|
At Int. suppt.: 2-#5 |
1-#5 |
@ 3.5”c/c |
||||||||
|
G.B-2 |
10”x10” |
7.72 |
8.82 |
13.72 |
0.23 |
0.27 |
0.43 |
At Ext. suppt: 2-#5 |
– |
@ 4.5”c/c |
|
At mid span : 2-#5 |
– |
@ 4.5”c/c |
||||||||
|
At Int. suppt.: 2-#5 |
– |
@ 4.5”c/c |
||||||||
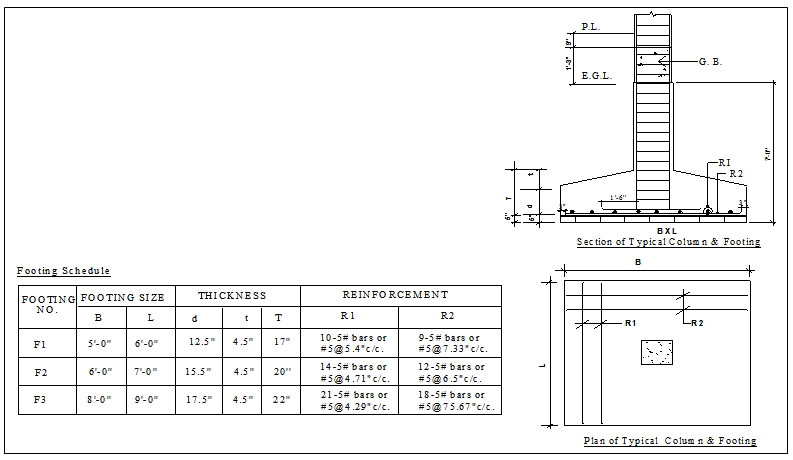
Design of footing:f all footings is given in Appendix XII. Analysis and design of one of the heavily loaded footing group (F-3) is presented below.
Design data:
Materials: = 60 ksi
= 3 ksi
= 150 pcf
Unit wt. of = 100 pcf
Allowable soil pressure = 4.5 ksf
Footing (F-3):
Depth of base below GL = 5’
l) Load calculation:
Weight coming from column C-3 = 322 k
Weight coming from GB-1 =
Weight coming from GB-2 =
Self weight of footing 10% of (1+2) = 34.40 k
Pu = 322+13.2+8.82+34.40 = 378.42 k
Unfactored load =
II) ‘d’ Check
Check for “d” (one way shear)
So ok.
Check for “d” (Two way shear)
So ok.
| III) Design of steel |
Short direction
Long direction:
A detail of sectional dimensions and reinforcement arrangement of all footings (F -1 ~ F-3) are given in Table 5.5 and Figure 5.6.
Bar arrangement, cut-off and bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Table 5.5: Details of sectional dimensions and reinforcement arrangement of all footings (F -1 ~ F-3)
|
Footing group |
Number of footing |
Footing size |
Footing load (kip) |
Moment (k-ft) |
Area of steel req. (sq. inch) |
Quantity of bars |
|||
|
Short direction |
Long direction |
Short direction (Ast) |
Long direction (Ast) |
Short direction |
Long direction |
||||
|
F-1 |
04 |
140.12 |
50.50 |
93.25 |
2.50 |
3.00 |
9-#5 |
10-#5 |
|
|
F-2 |
10 |
227.71 |
108.23 |
170.73 |
3.72 |
4.34 |
12-#5 |
14-#5 |
|
|
F-3 |
04 |
378.42 |
322.69 |
289.39 |
5.54 |
6.23 |
18-#5 |
21-#5 |
|
Details of dimensions and reinforcement arrangement of all footings (F -1 ~ F-3)
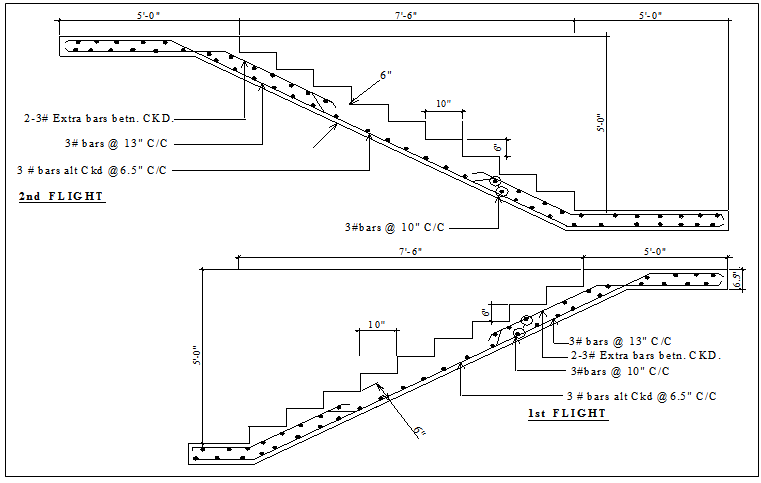
Design of Stair
Design Data
Materials:
= 60 ksi
= 3 ksi
= 150 pcf
Effective span of length = 12.5’
Tread = 10”
Rise = 6”
Loading:
Floor finish = 30 psf.
LL = 100 psf.
l) Load calculation:
Assume thickness of waist slab = 6’’
Effective d = 6’’- 1’’ = 5’’ and inclination of the waist slab, Ө = tan -1
Self load of waist slab
Self wt of steps lb / ft
Floor Finish = 30 lb / ft
DL = 90.14+41.67+30 = 161.81 lb / ft
Factored load = 1.2DL+1.6LL =1.20´161.81+1.6´100=354.17 lb / ft
ll) d check:
Positive Moment
Negative Moment
So ok.
lll) Design of steel:
For Positive Moment:
Use #3 bar which area = 0.11
Spacing
Use # 3 bar@ .
For Negative Moment:
Here, CKD to CKD @13”c/c
So, Req. steel
Use 2#3 Extra Bar between Cranked.
Temperature and shrinkage
Use #3bar which area = 0.11
Spacing
Use # 3 bars@.
Details of reinforcement arrangement of stair is shown in Figure 5.7.
Bar arrangement, cut-off and bent up, bar spacing etc. are done as per discussions and ACI/BNBC Codes provisions presented in Chapter III.
Thesis Paper On Longer Span Floor Beams System Of Edge Supported Structures(part 1)
Thesis Paper On Longer Span Floor Beams System Of Edge Supported Structures(part 2)