Analysis Between a Beam Supported Structure and a Flat Plate Structure (Part 2)

Shear reinforcement design:

V_s = V_u – φV_c

= 40.84 – (2 * 0.85√3500 * 10 * 16) / 1000 = 24.78 kip

4 √f_c   b_w d = (4√3500 * 10 * 16) / 1000 = 32.183 kip

V_s < 4√f_c      b_w d    So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 16 / 2 = 8”

3)      S_max = 24”

4)      S = φ A_vf_y d / V_s=  0.85 * 2 * 0.11 * 60000 * 16 / (24.78 * 1000) = 7.24”

Use stirrups # 3 bar @ 7” c/c

Design of the beam: B₁₃, B₁₅, B₁₆, B₁₈, B₁₉, B₂₁, B₂₂, B₂₄  (at 4th story)

From load combination:

Maximum moment at end section

Negative moment = 64.59 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f’_c)

d² = M_u / (фρf_y bd (1- 0.59 ρf / f’_c)

ρ _max = 0.75 ρ_b,   ρ_b = 0.85 β₁ f’_c / f_y  * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 64.59 * 12 / 0.90 * 0.0187 * 60 * 10 (1-0.59 * 0.0187 * 60 / 3.50)

d = 9.72, Clear cover = 2”, Total depth = 9.72 + 2= 11.72.  Say, d = 12”

Provided Beam size = 12” * 10”, d = 12”- 2”= 10”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 64.59 * 12 / 0.90 * 60 (10 – 1 / 2) = 1.51 in², a = A_sf_y / 0.85f^’_c   b_w

a = 1.51 * 60 / 0.85 * 3.50 * 10 = 3.045

As = 64.59 * 12 / 0.90 * 60 (10 – 3.045 / 2) = 1.693 in²

a = 1.693 * 60 / 0.85 * 3.5 * 10 = 3.414 in.

As = 64.59 * 12 / 0.90 * 60 (10 – 3.414 / 2) = 1.73 in².  Use – 2 # 7 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 51.98 * 12 / 0.90 * 60 (10 – 1 / 2) = 1.215 in², a = A_sf_y / 0.85f’_c b_w

a = 1.215 * 60 / 0.85 * 3.50 * 10 = 2.450 in.

A_s = 51.98 * 12 / 0.90 * 60 (10 – 2.45 / 2) = 1.316 in²

a = 1.316 * 60 / 0.85 * 3.50 * 10 = 2.609 in.

A_s = 51.98 * 12 / 0.90 * 60 (10 – 2.609 / 2) = 1.328 in².  Use – 2 # 6 +2 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 25.40 – (2 * 0.85√3500 * 10 * 10) / 1000 = 15.34 kip

4 √f_c   b_w d = (4√3500 * 10 * 10) / 1000 = 23.66 kip

V_s < 4√f_c    b_w d   So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 10 / 2 = 5”

3)      S_max = 24”

4)     S =  φ A_vf_y d / V_s =  0.85 * 2 * 0.11 * 60000 * 10 / (15.34*1000) = 7.31 ”

Use stirrups # 3 bar @ 5” c/c

Design of the beam: B₁, B₃,B₄, B₆, B_7, B₉, B₁₀, B₁₁  ( at 4th story )

From load combination:

Maximum moment:

End section:

Negative moment = 87.25 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u/ фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max =  0 .75 ρ_b, ρ_b = 0.85 β₁ f’_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 87.25 * 12 / 0.90 * 0.0187 * 60 * 10 (1- 0.59 * 0.0187 * 60 / 3.50)

d = 11.29, Clear cover = 2”, Total depth = 11.29 + 2= 13.29.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 87.25 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.551 in², a = A_sf_y / 0.85f_c   b_w

a = 1.551 * 60 / 0.85 * 3.50 * 10 = 3.128 in.

A_s = 87.25 * 12/0.90 * 60 (13 – 3.128 / 2) = 1.695 in²

a = 1.695 * 60 / 0.85 * 3.50 * 10= 3.418 in.

A_s = 87.25 * 12 / 0.90 * 60 (10 – 3.418 / 2) = 1.717 in².  Use – 2 # 7 + 2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 35.0 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.622 in², a = A_sf_y / 0.85f’_c b_w

a = 0.622 * 60 / 0.85 * 3.50 * 10 = 1.254 in.

A_s = 35.00 * 12 / 0.90 * 60 (13 – 1.254 / 2) = 0.628 in²

a = 0.628 * 60 / 0.85 * 3.50 * 10 = 1.266 in.

A_s = 35.0 * 12 / 0.90 * 60 (13 – 1.266/2) = 0.63 in². Use – 2 # 6 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 22.23 – (2 * 0.85√3500 * 10 * 13) / 1000 = 9.15 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) /1000 = 30.76 kip

V_s < 4√f_c   b_w d    So, ok

Stirrup spacing:

1)   S_max = A_vf_y / 50   b_w = (2 * 0.11* 60000) / 50 * 10 = 26.40”

2)   S_max = d / 2 = 13 / 2 = 6½”

3)   S_ma   = 24”

4)   S = φ A_vf_y d / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (9.15 * 1000) = 15.94”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₂, B₅, B₈, B₁₂  ( at  4th story )

From load combination:

Maximum moment:

End section:

Negative moment = 108.93 k-ft

M_u = ф ρfy bd² (1- 0.59 ρf_y / f_c)

d² = M_u / фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β1 f_c / f_y *  87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 108.93 * 12 / 0.90 * 0.0187 * 60 * 10(1- 0.59 * 0.0187 * 60 / 3.50)

d = 12.63, Clear cover = 2”, Total depth = 12.63 + 2 = 14.63.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 108.93 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.936 in², a = A_sf_y / 0.85f_c   b_w,

a = 1.936 * 60 / 0.85 * 3.50 * 10 = 3.904 in.

As = 108.93 * 12 / 0.90 * 60 (13 – 3.904 / 2) = 1.867 in²

a = 1.897 * 60 / 0.85 * 3.50 * 10 = 3.765 in.

As = 108.93 * 12 / 0.90 * 60 (13 – 3.765 / 2) = 2.177 in². Use – 2 # 8 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 59.56 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.058 in², a = A_sf_y / 0.85f_c   b_w,

a = 1.058 * 60 / 0.85 * 3.50 * 10 = 2.133 in.

A_s = 59.56 * 12 / 0.90 * 60 (13 – 2.133 / 2) = 1.108 in²

a = 1.108 * 60 / 0.85 * 3.5 * 10 = 2.234 in.

A_s = 59.56 * 12 / 0.90 * 60 (13 – 2.234 / 2) = 1.113in². Use – 4 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 26.90 – (2 * 0.85√3500 * 10 * 13) / 1000 = 13.825 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763 kip

V_s < 4√f_c   b_w d   So, ok

Stirrups Spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 13 / 2 = 6½”

3)      S_max = 24”

4)      S = φ A_vf_yd / V_s =  0.85 * 2 * 0.11 * 60000 * 13 / (13.825 * 1000) = 10.55”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁₄, B₁₇, B₂₀, B₂₃  (at 4th story)

From load combination:

Maximum Moment:

End section:

Negative moment = 164.32 k-ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / (ф ρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,    ρ_b = 0.85 β₁ f_c / f_y  *  87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ_max = 0.75 * 0.02494 = 0.0187

d² = 164.32 *12 / 0.90 * 0.0187 * 60 * 12 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 14.16, Clear cover = 2”, Total depth = 14.16 + 2 = 16.16.  Say, d = 18”

Provided Beam size = 18” * 10”, d = 18”- 2”= 16”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 164.32 * 1 / 0.90 * 60 (16 – 1 / 2) = 2.355 in², a = A_sf_y / 0.85f_c   b_w,

a = 2.355 * 60 / 0.85 * 3.50 * 12 = 3.957 in.

A_s = 164.32 * 12 / 0.90 * 60 (16 – 3.597 / 2) = 2.604 in²

a = 2.604 * 60 / 0.85 * 3.50 * 10 = 4.376 in.

A_s = 164.32 * 12 / 0.90 * 60 (16 – 4.376 / 2) = 2.643 in².  Use – 2 # 9 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 103.66 * 12 / 0.90 * 60 (16 – 1 / 2) = 1.49 in², a = A_sf_y / 0.85f_c   b_w,

a = 1.49 * 60 / 0.85 * 3.5 * 10 = 3.00 in.

A_s = 103.66 * 12 / 0.90 * 60 (16 – 3.00 / 2) = 1.59 in²

a = 1.59 * 60 / 0.85 * 3.50 * 10 = 3.206 in.

As = 103.66 * 12 / 0.90 * 60 (16 – 3.206 / 2) = 1.60 in². Use – 2 # 7 +2 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 43.60 – (2 * 0.85√3500 * 10 * 16) / 1000 = 24.28 kip

4 √f_c     b_w d = (4√3500 * 12 * 16) / 1000 = 45.435 kip

V_s < 4√f_c   b_w d    So, ok

 Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w =  (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)     S_max = d / 2 = 16 / 2 = 8”

3)      S_max = 24”

4)      S =  φA_vf_y d / V_s =  0.85 * 2 * .11 * 60000 * 16 / (24.28 * 1000) = 7.39 ”

Use stirrups # 3 bar @ 7” c/c

Design of the beam: B₁₃, B₁₅, B₁₆, B₁₈, B₁₉, B₂₁, _B22, B₂₄  (at 4th story)

From load combination:

Maximum moment at end section

Negative moment = 115.36 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / (ф ρf_y bd (1- 0.59 ρf / f_c)

ρ _max = 0.75 ρ_b,   ρ_b = 0.85 β₁ f_c / f_y *  87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 115.36 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 13.0, Clear cover = 2”, Total depth = 13 + 2 = 15.0.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 115.36 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.05 in², a = A_sf_y / 0.85f_c   b_w.

a = 2.05 * 60 / 0.85 * 3.50 * 10 = 4.134 in

A_s = 115.36 * 12 / 0.90 * 60 (13 – 4.134 / 2) = 2.344 in²

a = 2.344 * 60 / 0.85 * 3.5 * 10 = 4.727 in.

A_s = 115.36 * 12 / 0.90 * 60 (13 – 4.727 / 2) = 2.41 in².  Use – 2 # 8 +2 # 6 bars

 Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 48.69 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.865 in², a = A_sf_y / 0.85f_c   b_w,

a = 0.865 * 60 / 0.85 * 3.50 * 10 = 1.744 in

A_s = 48.69 * 12 / 0.90 * 60 (13-1.744/2) = 0.892 in²

a = 0.892 * 60 / 0.85 * 3.50 * 10 = 1.798 in.

A_s = 48.69 * 12 / 0.90 * 60 (13 – 1.798 / 2) = 0.894 in². Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 32.18 – (2 * 0.85√3500 * 10 * 13) / 1000 = 19.10 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763kip

V_s < 4√f_c   b_w d   So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)     S_max = d / 2 = 13 / 2 = 6½”

3)      S_max = 24”

4)      S =  φ A_vf_y d / V_s =  0.85 * 2 * .11 * 60000 * 13 / (19.10 * 1000) = 7½ ”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁, B₃, B₄, B₆, B₇, B₉, B₁₀, B₁₁  ( at 3rd  story )

From load combination:

Maximum moment:

End section:

Negative moment = 87.25 k-ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,    ρ_b = 0.85 β₁ f_c / f_y *  87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.50 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ_max = 0.75 * 0.02494 = 0.0187

d² = 87.25 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 11.29, Clear cover = 2”, Total depth = 11.29+2 = 13.29.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 87.25 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.551 in², a = A_sf_y / 0.85f_c   b_w,

a = 1.551 * 60 / 0.85 * 3.50 * 10 = 3.128 in.

A_s = 87.25 * 12 / 0.90 * 060 (13 – 3.128 / 2) = 1.695 in²

a = 1.695 * 60 / 0.85 * 3.5 * 10 = 3.418 in.

A_s = 87.25 * 12 / 0.90 * 60 (10 – 3.418 / 2) = 1.717 in².  Use – 2 # 7 +2 # 5 bars

 Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 35.0 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.622 in², a = A_sf_y / 0.85f’_c b_w

a = 0.622 * 60 / 0.85 * 3.50 * 10 = 1.254 in.

A_s = 35.00 * 12 / 0.90 * 60 (13 – 1.254 / 2) = 0.628 in²

a = 0.628 * 60 / 0.85 * 3.50 * 10 = 1.266 in.

A_s = 35.0 * 2 / 0.90 * 60 (13 – 1.266 / 2) = 0.63 in². Use – 2 # 6 bars

 Shear reinforcement design:

V_s = V_u – φV_c

= 22.23 – (2 * 0.85√3500 * 10 * 13) / 1000 = 9.15 kip

4 √fc b_w d = (4√3500 * 10 * 13) / 1000 = 30.76 kip

V_s < 4√f_c b_w d   So, ok

Stirrup spacing:

1)   S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)   S_max = d / 2 = 13 / 2 = 6½”

3)   S_max = 24”

4)   S = φ A_vf_yd / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (9.15 * 1000) =15.94

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₂, B₅, B₈, B₁₂  ( at  3rd  story )

From load combination:

Maximum moment at end section

Negative moment = 108.93 k-ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,   ρ_b = 0.85 β₁ f_c / f_y *  87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 108.93 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 12.63, Clear cover = 2”, Total depth = 12.63+2= 14.63.  Say, d = 15

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 108.93 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.936 in², a = A_sf_y / 0.85f_c   b_w.

a = 1.936 * 60 / 0.85 * 3.50 * 10 = 3.904 in.

A_s = 108.93 * 12 / 0.90 * 60 (13 – 3.904 / 2) = 1.867 in²

a = 1.897 * 60 / 0.85 * 3.5 * 10 = 3.765 in

A_s = 108.93 * 12 / 0.90 * 60 (13-3.765 / 2)   = 2.177 in².  Use – 2 # 8 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 59.56 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.058 in², a = A_sf_y / 0.85f_c   b_w

a = 1.058 * 60 / 0.85 * 3.5 * 10 = 2.133 in.

A_s = 59.56 * 12 / 0.90 * 60 (13 – 2.133 / 2) = 1.108 in²

a = 1.108 * 60 / 0.85 * 3.50 * 10 = 2.234 in.

A_s = 59.56 * 10.90 * 6 (13 – 2.234 / 2) = 1.113in².  Use – 4 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 26.90 – (2 * 0.85√3500 * 10 * 13) / 1000 = 13.825 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763 kip

V_s < 4√f_c   b_w d.    So, ok

Stirrup spacing:

1)   S_max = A_vf_y / 50   b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)   S_max = d / 2 = 13 / 2 = 6½”

3)   S_max = 24”

4)  S = φ A_vf_yd / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (13.825 * 1000) = 10.55”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁₄, B_17, B₂₀, B₂₃  ( at 3rd  story )

From load combination:

Maximum moment at end section

Negative moment = 164.32 k-ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / (фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b, ρ_b = 0.85 β₁ f’_c / fy * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ_max = 0.75 * 0.02494 = 0.0187

d² = 164.32 * 12 / 0.90 * 0.0187 * 60 * 12 (1-0.59 * 0.0187 * 60 / 3.50)

d = 14.16, Clear cover = 2”, Total depth = 14.16+2 = 16.16.  Say, d = 18”

Provided Beam size = 18” * 10”, d = 18”- 2”= 16”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 164.32 * 12 / 0.90 * 60 (16 – 1 / 2) = 2.355 in², a = A_sf_y / 0.85fc b_w

a = 2.355 * 60 / 0.85 * 3.50 * 12 = 3.957 in.

A_s = 164.32 * 12 / 0.90 * 60 (16 – 3.597 / 2) = 2.604 in²

a = 2.604 * 60 / 0.85 * 3.5 * 10 = 4.376 in.

A_s = 164.32 * 12 / 0.90 * 60 (16 – 4.376 / 2) = 2.643 in².  Use – 2 # 9 +5 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 103.66 * 12 / 0.90 * 60 (16 – 1 / 2) = 1.49 in², a = A_sf_y / 0.85f_c    b_w

a = 1.49 * 60 / 0.85 * 3.5 * 10 = 3.00 in.

A_s = 103.66 * 12 / 0.90 * 60 (16 – 3.00 / 2) = 1.59 in²

a = 1.59 * 60 / 0.85 * 3.50 * 10 = 3.206 in.

A_s = 103.66 * 12 / 0.90 * 60 (16 – 3.206 / 2) = 1.60 in².  Use – 2 # 7 +2 # 5 bars

 Shear reinforcement design:

V_s = V_u – φV_c

= 43.60 – (2 * 0.85√3500 * 10 * 16) / 1000 = 24.28 kip

4 √f_c b_w d = (4√3500 * 12 * 16) / 1000 = 45.435 kip

V_s < 4√f_c b_w d   So, ok

Stirrup spacing:

1)   S_max = A_vf_y / 50   b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)   S_max = d / 2 = 16 / 2 = 8”

3)   S_max = 24”

4)   S = φ A_vf_y d / V_s = 0.85 * 2 * 0.11 * 60000 * 16 / (24.28 * 1000) = 7.39 in

Use stirrups # 3 bar @ 7” c/c

Design of the beam: B₁₃, B₁₅, B₁₆, B₁₈, B₁₉, B₂₁, B₂₂, B₂₄  (at 3rd story)

From load combination:

Maximum moment at end section

Negative moment = 115.36 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / (фρf_y bd (1- 0.59 ρf_y / f’_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β₁ f_c  / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000+60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 115.36 * 12 / 0.90 * 0.0187 * 60 *10 (1- 0.59 * 0.0187 * 60 / 3.50)

d = 13.0, Clear cover = 2”, Total depth = 13+2 = 15.0.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 115.36 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.05 in², a = A_sf_y / 0.85f_c    b_w.

a = 2.05 * 60 / 0.85*3.5*10 = 4.134 in.

A_s = 115.36 * 12 / 0.90 * 60 (13 – 4.134 / 2) = 2.344 in.²

a = 2.344 * 60 / 0.85 * 3.5 * 10 = 4.727 in.

A_s = 115.36 * 12 / 0.90 * 60 (13 – 4.727 / 2) = 2.41 in².  Use – 2 # 8 +2 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 48.69 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.865 in², a = A_sf_y / 0.85f_c   b_w,

a = 0.865 * 60 / 0.85 * 3.50 * 10 = 1.744 in.

A_s = 48.69 * 12 / 0.90 * 60 (13 – 1.744 / 2) = 0.892 in²

a = 0.892 * 60 / 0.85 * 3.5 * 10 = 1.798 in

A_s = 48.69 * 12/0.90 * 60 (13 – 1.798 / 2) = 0.894 in².  Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 32.18 – (2 * 0.85√3500 * 10 * 13) / 1000 = 19.10 kip

4 √f_c   b_w d = (4√3500 *10 * 13) / 1000 = 30.763kip

V_s < 4√f_c    b_w d   So, ok

Stirrup spacing:

1)   S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)    S_max = d / 2 = 13 / 2 = 6½”

3)    S_max = 24”

4)    S = φ A_vf_y d / V_s = 0.85 * 2 * .11 * 60000 * 13 / (19.10 * 1000) = 7½”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁, B₃, B₄, B₆, B₇, B₉, B₁₀, B₁₁  ( at 2nd  story )

From load combination:

Maximum moment at end section

Negative moment = 89.0 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / ф ρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,   ρ_b = 0.85 β₁ f_c / fy  * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 89.00 * 12 / 0.90 * 0.0187 * 60 * 12 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 10.42, Clear cover = 2”, Total depth = 10.42+2 = 12.42.  Say, d = 15”

Provided Beam size = 15” * 12”, d = 15”- 2”= 13”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 89.00 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.582 in², a = A_sf_y / 0.85f_c b_w

a = 1.582 * 60 / 0.85 * 3.50 * 12 = 2.658 in.

A_s = 89.0 * 12 / 0.90 * 60 (13 – 2.658 / 2) = 1.694 in²

a = 1.694 * 60 / 0.85 * 3.50 * 10 = 2.847 in.

A_s = 89.0 * 12 / 0.90 * 60 (13 – 2.847 / 2) = 1.708 in².  Use – 4 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 42.26 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.751 in², a = A_sf_y / 0.85f_c   b_w

a = 0.751 * 60 / 0.85 * 3.50 * 10 = 1.514 in.

A_s = 42.26 * 12 / 0.90 * 60 (13 – 1.514 / 2) = 0 .767 in²

a = 0.767 * 60 / 0.85 * 3.50 * 10 = 1.546 in.

A_s = 42.26 * 12 / 0.90 * 60 (13 – 1.546 / 2) = 0.768 in².  Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 23.17 – (2 * 0.85√3500 * 10 * 13 / 1000 = 10.10 kip

4 √f_c    b_w d = (4√3500 * 10 * 13) / 1000 = 30.76 kip

V_s < 4√f_c   b_w d   So, ok

Stirrup spacing:

1)      S_max = A_vf_y/ 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 13 / 2 = 6½”

3)      S_max = 24”

4)      S = φ A_vf_y d / V_s =  0.85 * 2 * 0.11 * 60000 * 13 / (10.10 * 1000) = 14.44”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₂, B₅, B₈, B₁₂  ( at  2nd  story )

From load combination:

Maximum moment at end section

Negative moment = 114.44 k – ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / ф ρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β₁ f’_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187.

d² = 114.44 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50).

d = 12.95, Clear cover = 2”, Total depth = 12.95+2 = 14.95.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

 Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 114.44 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.034 in², a = A_sf_y / 0.85f_c   b_w

a = 2.034 * 60 / 0.85 * 3.50 * 10 = 4.102 in.

A_s = 114.44 * 12 / 0.90 * 60 (13 – 4.102 / 2) = 2.322 in²

a = 2.322 * 60 / 0.85 * 3.50 * 10 = 4.683 in.

A_s = 114.44 * 12 / 0.90 * 60 (13 – 4.683 / 2) = 2.386 in².  Use – 2 # 9 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 60.52 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.075 in², a = A_sf_y / 0.85f_c   b_w

a = 1.075 * 60 / 0.85 * 3.50 * 10 = 2.168 in.

A_s = 60.52 * 12 / 0.90 * 60 (13 – 2.168 / 2) = 1.128 in²

a = 1.128 * 60 / 0.85 * 3.50 * 10 = 2.274 in.

A_s = 60.52 * 12 / 0.90 * 60 (13 – 2.274 / 2) = 1.133 in².  Use – 4 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 24.47 – (2 * 0.85√3500 * 10 * 13) / 1000 = 17.412 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763 kip

V_s < 4√f_c    b_w d    So, ok

Stirrups Spacing:

1)   S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)   S_max = d / 2 = 13 / 2 = 6½”

3)   S_max = 24”

4)   S = φ A_vf_y d / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (17.412 * 1000) = 8.37”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁₄, B₁₇, B₂₀, B₂₃  ( at  2nd  story )

From load combination:

Maximum moment at end section

Negative moment = 169.91 k-ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / (ф ρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β1 fc / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 169.91 * 12 / 0.90 * 0.0187 * 60 * 12 (1-0.59 * 0.0187 * 60 / 3.50)

d = 14.40, Clear cover = 2”, Total depth = 14.40+2 = 16.40.  Say, d = 18”

Provided Beam size = 18” * 12”, d = 18”- 2”= 16”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 169.91 * 12 / 0.90 * 60 (16 – 1 / 2) = 2.43 in², a = A_sf_y / 0.85f_c b_w

a = 2.43 * 60 / 0.85 * 3.50 * 12 = 4.08 in.

A_s = 169.91*12 / 0.90 * 60 (16 – 4.08 / 2) = 2.70 in²

a = 2.70 * 60 / 0.85 * 3.50 * 12 = 4.54 in.

A_s = 169.91 * 12 / 0.90 * 60 (16 – 4.54 / 2 = 2.75 in².  Use – 2 # 9 +2 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 104.10 *12 / 0.90 * 60 (16 – 1 / 2) = 1.49 in², a = A_sf_y / 0.85f_c b_w

a = 1.49 * 60 / 0.85 * 3.50 * 10 = 3.00 in.

A_s = 104.10 * 12 / 0.90 * 60 (16 – 3.00 / 2) = 1.59 in²

a = 1.59 * 60 / 0.85 * 3.50 * 10 = 3.206 in.

A_s = 104.10 * 12 / 0.90 * 60 (16 – 3.206 / 2) = 1.60 in².  Use – 2 # 7 +2 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 44.19 – (2 * 0.85√3500 * 12 * 16) / 1000 = 24.88 kip

4 √f_c    b_w d = (4√3500 * 12 * 16) / 1000 = 45.435 kip

V_s < 4√f_c   b_w d   So, ok

Stirrup spacing:

1)     S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)     S_max = d / 2 = 16 / 2 = 8”

3)     S_max = 24”

4)     S = φA_vf_y d / V_s = 0.85 * 2 * 0.11 * 60000 * 16 / (24.88 * 1000) =7.21 ”

Use stirrups # 3 bar @ 7” c/c

Design of the beam: B₁₃, B₁₅, B₁₆, B₁₈, B₁₉, B₂₁, B₂₂, B₂₄  (at  2nd  story)

From load combination:

Maximum moment at end section

Negative moment = 114.84 k-ft

M_u = ф ρf_y bd² (1- 0.59 ρf_y / f_c)

d² = M_u / (фρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β₁ f_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 114.84 *12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 12.97, Clear cover = 2”, Total depth = 12.97+2= 14.97

Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 114.84 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.041 in², a = A_sf_y / 0.85f_c   b_w.

a = 2.041*60 / 0.85*3.5*10 = 4.116 in.

A_s = 114.84 * 12 / 0.90 * 60 (13 – 4.116 / 2) = 2.332 in²

a = 2.332 * 60 / 0.85 * 3.5 * 10 = 4.703 in.

A_s = 114.84 * 12 / 0.90 * 60 (13 – 4.703 / 2) = 2.396 in². Use – 2 # 8 +2 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 51.04 * 12 / 0.90 * 60 (13 – 1 / 2) = 0 .907 in², a = A_sf_y / 0.85f_c b_w,

a = 0.907 * 60 / 0.85 * 3.5 * 10 = 1.829 in.

A_s = 51.04 * 12 / 0.90 * 60 (13 – 1.829 / 2) = 0.938 in²

a = 0.938 * 60 / 0.85 * 3.50 *10 = 1.891 in.

A_s = 51.04 * 12 / 0.90 * 60 (13 – 1.891 / 2) = 0.941 in².  Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 32.71- (2 * 0.85√3500 * 10 * 13) / 1000 = 18.92 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763kip

V_s < 4√f_c   b_w d   So, ok

 Stirrup spacing:

1)    S_max   = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)    S_max = d / 2 = 13 / 2 = 6½”

3)    S_max = 24”

4)    S = φ A_vf_yd / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (18.92 * 1000) = 7.71”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁, B₄, B₆, B₇, B₉, B₁₀, B₁₁  ( at 1st  story )

From load combination:

Maximum moment at end section

Negative moment = 89.0 k – ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / ф ρf_y bd (1- 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b,  ρ_b = 0.85 β_{1 f}’_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 89.00 * 12 / 0.90 * 0.0187 * 60 * 12 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 10.42, Clear cover = 2”, Total depth = 10.42+2 =12.42.  Say, d = 15”

Provided Beam size = 15” * 12”, d = 15”- 2” = 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 89.00 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.582 in², a = A_sf_y / 0.85f_c   b_w.

a = 1.582 * 60 / 0.85 * 3.5 * 12 = 2.658 in.

A_s = 89.0 * 12 / 0.90 * 60 (13 – 2.658 / 2) = 1.694 in²

a = 1.694 * 60 / 0.85 * 3.50 * 10 = 2.847 in.

A_s = 89.0 * 12 / 0.90 * 60 (13 – 2.847 / 2) = 1.708 in².  Use – 4 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 42.26 * 12 / 0.90 * 60 (13 – 1 / 2) = 0.751 in², a = A_sf_y / 0.85f_c   b_w.

a = 0.751 * 60 / 0.85 * 3.5 * 10 = 1.514 in.

A_s = 42.26 * 12 / 0.90 * 60 (13 – 1.514 / 2) = 0.767 in²

a = 0.767 * 60 / 0.85 * 3.50 * 10 = 1.546 in

A_s = 42.26 * 12 / 0.90 * 60 (13 – 1.546 / 2) = 0.768 in².  Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 23.17 – (2 * 0.85√3500 * 10 * 13) / 1000 = 10.10 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.76 kip

V_s < 4√f_c b_w d    So, ok

Stirrup spacing:

1)     S_max = A_vf_y / 50 b_w= (2 * 0.11 * 60000 ) / 50 * 10 = 26.40”

2)     S_max = d / 2 = 13 / 2 = 6½”

3)     S_max = 24”

4)     S =  φA_vf_y d / V_s = 0.85 * 0.11 * 60000 * 13 / (10.10 * 1000) =14.44”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₂, B₅, B₈, B₁₂  ( at  1st  story )

From load combination:

Maximum moment at end section

Negative moment = 114.44 k – ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / ф ρf_y bd (1 – 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b ,  ρ_b = 0.85 β₁ f_c / fy * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ_max = 0.75 * 0.02494 = 0.0187

d² = 114.44 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 12.95, Clear cover = 2”, Total depth = 12.95+2 = 14.95. Say, d = 15 “

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 114.44 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.034 in², a = A_sf_y / 0.85f_c    b_w

a = 2.034 * 60 / 0.85 * 3.5 * 10 = 4.102 in.

A_s = 114.44 * 12 / 0.90 * 60 (13 – 4.102 / 2) = 2.322 in²

a = 2.322 * 60 / 0.85 * 3.5 * 10 = 4.683 in

A_s = 114.44 * 12 / 0.90 * 60 (13 – 4.683 / 2) = 2.386 in².  Use – 2 # 9 +2 # 5 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 60.52 * 12 / 0.90 * 60 (13 – 1 / 2) = 1.075 in², a = A_sf_y / 0.85f_c b_w

a = 1.075 * 60 / 0.85 * 3.5 * 10 = 2.168 in.

A_s = 60.52 * 12 / 0.90 * 60 (13 – 2.168 / 2) = 1.128 in²

a = 1.128 * 60 / 0.85 * 3.50 * 10 = 2.274 in

A_s = 60.52 * 12 / 0.90 * 60 (13 – 2.274 / 2) = 1.133 in².  Use – 4 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 24.47 – (2 * 0.85√3500 * 10 * 13) / 1000 = 17.412 kip

4 √f_c   b_w d = (4√3500 * 10 * 13) / 1000 = 30.763 kip

V_s < 4√f_c    b_w d    So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 13 / 2 = 6½”

3)      S_max = 24”

4)      S =  φ A_vf_y d / V_s = 0.85 * 2 * 0.11 * 60000 * 13 / (17.412 * 1000) = 8.37”

Use stirrups # 3 bar @ 6½” c/c

Design of the beam: B₁₄, B₁₇, B₂₀, B₂₃  ( at  1st  story )

From load combination:

Maximum moment at mid section

Negative moment = 169.91 k – ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / (фρf_y bd (1 – 0.59 ρf_y / f_c)

ρ _max = 0.75 ρ_b ,  ρ_b = 0.85 β₁ f_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 169.91 * 12 / 0.90 * 0.0187 * 60 * 12 (1- 0.59 * 0.0187 * 60 / 3.50)

d =14.40, Clear cover = 2”, Total depth = 14.40+2= 16.40.  Say, d = 18”

Provided Beam size = 18” * 12”, d = 18”- 2”= 16”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 169.91 * 12 / 0.90 * 60 (16 -1 /2) = 2.43 in², a = A_sf_y / 0.85f_c   b_w.

a = 2.43 * 60 / 0.85 * 3.5 * 12 = 4.08

A_s = 169.91 * 12 / 0.90 * 60 (16 – 4.08 / 2) = 2.70 in²

a = 2.70 * 60 / 0.85 * 3.5 * 12 = 4.54 in.

A_s = 169.91 * 12 / 0.90 * 60 (16 – 4.54 / 2) = 2.75 in².   Use – 2 # 9 +2 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 104.10 * 12 / 0.90 * 60 (16 – 1 / 2) = 1.49 in², a = A_sf_y / 0.85f’_c   b_w

a = 1.49 * 60 / 0.85 * 3.5 * 10 = 3.0 in

A_s = 104.10 * 12 / 0.90 * 60 (16 – 3.00 / 2) = 1.59 in²

a = 1.59 * 60 / 0.85 * 3.50 *10 = 3.206 in.

A_s = 104.10 * 12 / 0.90 * 60 (16 – 3.206 / 2) = 1.60 in².  Use – 2 # 7 +2 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 44.19 – (2 * 0.85√3500 * 12 * 16) / 1000 = 24.88 kip

4 √f_c   b_w d = (4√3500 * 12 * 16) / 1000 = 45.435 kip

V_s < 4√f_c   b_w d   So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0 .11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 16 / 2 = 8”

3)      S_max = 24”

4)      S =  φ A_vf_yd /  V_s =  0.85 * 2 * 0.11 * 60000 * 16 / (24.88 * 1000) = 7.21 ”

Use stirrups # 3 bar @ 7” c/c

Design of the beam: B₁₃, B₁₅, B₁₆, B₁₈, B₁₉, B₂₁, B₂₂, B₂₄  (at 1st  story)

From load combination:

Maximum moment at end section

Negative moment = 114.84 k-ft

M_u = ф ρf_y bd² (1 – 0.59 ρf_y / f_c)

d² = M_u / (ф ρf_y bd (1 – 0.59ρf_y / f_c)

ρ _max = 0.75 ρ_b,   ρ_b = 0.85 β₁ f_c / f_y * 87000 / (87000 + 60000)

= 0.85 * 0.85 * 3.5 / 60 * 87000 / (87000 + 60000) = 0.02494

ρ _max = 0.75 * 0.02494 = 0.0187

d² = 114.84 * 12 / 0.90 * 0.0187 * 60 * 10 (1 – 0.59 * 0.0187 * 60 / 3.50)

d = 12.97, Clear cover = 2”, Total depth = 12.97+2 = 14.97.  Say, d = 15”

Provided Beam size = 15” * 10”, d = 15”- 2”= 13”

Main steel calculation:

A_s = M_u / φf_y (d – a / 2)

= 114.84 * 12 / 0.90 * 60 (13 – 1 / 2) = 2.041 in², a = A_sf_y / 0.85f_c   b_w

a = 2.041 * 60 / 0.85 * 3.5 * 10 = 4.116 in.

A_s = 114.84 * 12 / 0.90 * 60 (13 – 4.116 / 2) = 2.332 in²

a = 2.332 * 60 / 0.85 * 3.5 * 10= 4.703 in.

A_s = 114.84 * 12 / 0.90 * 60 (13 – 4.703 / 2) = 2.396 in².  Use – 2 # 8 +2 # 6 bars

Main steel calculation:

Mid section:

A_s = M_u / φf_y (d – a / 2)

= 51.04 * 12 / 0.90 * 60 (13 – 1 / 2) = 0 .907 in², a = A_sf_y / 0.85f_c   b_w

a = 0.907 * 60 / 0.85 * 3.5 * 10 = 1.829 in.

A_s = 51.04 * 12 / 0.90 * 60 (13 – 1.829 / 2) = 0.938 in²

a = 0.938 * 60 / 0.85 * 3.50 * 10 = 1.891 in.

A_s = 51.04 * 12 / 0.90 * 60 (13 – 1.891 / 2) = 0.941 in². Use – 3 # 5 bars

Shear reinforcement design:

V_s = V_u – φV_c

= 32.71 – (2 * 0.85√3500 * 10 * 13) / 1000 = 18.92 kip

4 √f_c   b_wd = (4√3500 *10 * 13) / 1000 = 30.763kip

V_s < 4√f_c   b_w d    So, ok

Stirrup spacing:

1)      S_max = A_vf_y / 50 b_w = (2 * 0.11 * 60000) / 50 * 10 = 26.40”

2)      S_max = d / 2 = 13 / 2 = 6½”

3)      S_max = 24”

4)      S =  φ A_vf_y d/ V_s =  0.85 * 2 * 0.11 * 60000 * 13 / (18.92 * 1000) = 7.71 ”

Use stirrups # 3 bar @ 6½” c/c

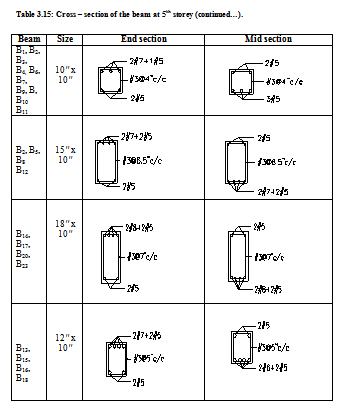
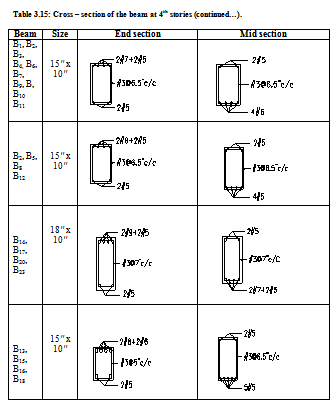
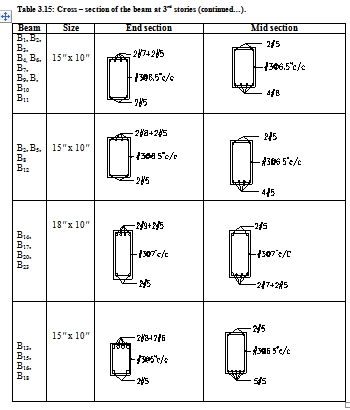
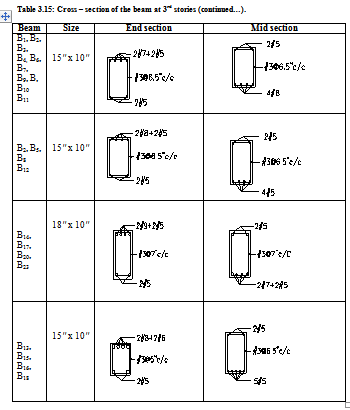
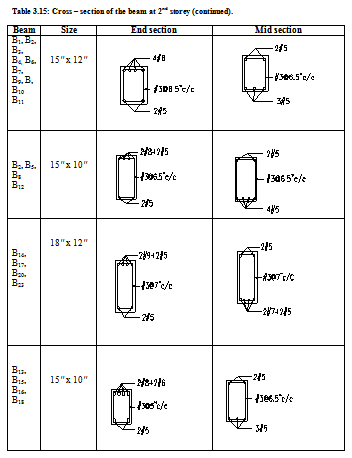
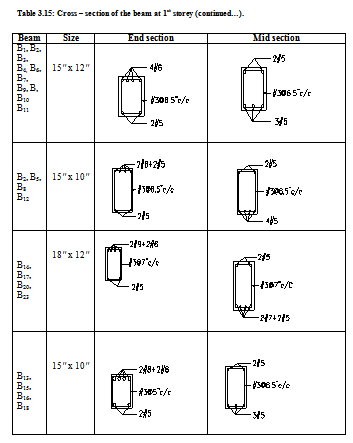
The table below is showing cross section of different floor beams at their end sections and mid section.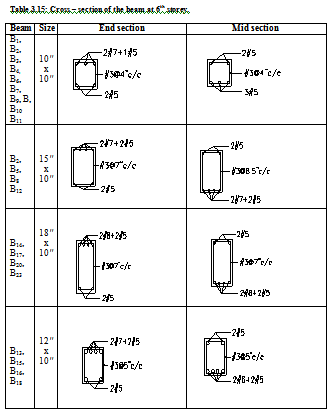

Column design for beam supported structure.

Design of the Column: C₁, C₄, C₁₀, C₁₆

From load combination:

P_u = 329.81 Kips = 329.81*1.20 = 396 Kips

Now,   P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g f_y)

Or   396 = 0.80 * 0.65 * A_g (0.85 * 3.5 (1- 0.025) + 0.025 * 60)

Or   396 = 2.288 A_g   Or    A_g = 173.076 in²  Or      A_g = 10” * 18”

Provided Column size = 10” * 18”,   A_g   = 180 in²

Main steel calculation:

P_u = α ф (0 .85 f’c (A_g – A) + A_sf_y)

Or    396 = 0.80 * 0.65 (0.85 * 3.5 (180 – A_s) + A_s * 60)

Or    396 = 278.46 – 1.547A_s + 31.20 A_s.    Or   A_s = 3.963 in²

Use 4 # 8 bars +2 # 6 bars,    A_s = 4.04 in²

 Tie design:

Spacing:  S = 16 D = 16 * 6 / 8 = 12” c/c,   S = 48 d = 48 * 3 / 8 = 18” c/c

At least lateral dimension,    S = 10” c/c.   Use # 3 bar ties @ 10” c/c.

Y – A_xis:

γ = 13 / 18 = 0.72,   e_x = M_x / P = 56.093 * 12 / 329.81= 2.04 in

e_y = M_y / P = 1.78 * 12/329.81 = 0.06 in, e_x / h = 2.04 / 18 = 0.113

Reinforcement Ratio:  ρ_g =A_s / A _g = 4.04 / 180 = 0.022

From Graph:   P_{n yo} / f′_c   A_g = 0.91

Or    P_{n yo} = 0.91 * 3.50 * 180 = 573.30 kips

P_o / f′_c A_g = 1.11   Or    P_o = 1.11 * 3.50 * 180 = 699.30 kips

X – A_xis:

γ = 5 / 10 = 0.5,    e_x = M_x / P = 56.093 * 12/329.81= 2.04 in

e_y = M_y  / P = 1.78*12 / 329.81 =  0.06 in, e_y / h = 0.06 / 10 = 0.006

Reinforcement ratio:    ρ_g =A_s / A _g = 4.04 / 180 = 0.022

From Graph:  P_{n xo} / f′_c A_g = 1.02

Or P_{n xo} = 1.02 * 3.50 * 180 = 642.60 kips

P_o /f′_c A_g = 1.11   Or    P_o = 1.11 * 3.50 * 180 = 699.30 kips

Here –   1 / P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or 1 / P_n = 1 / 642.60 + 1 / 573.30 – 1 / 699.30.  Or  P_n = 534.64 kips

Now,   P_u = ф P_n.    Or   P_u = 0.65 * 534.64

Or   P_u = 347.516 kips > 329.81 kips.   So design is ok.

Design of the Column : C₂, C₃, C_5, C₈, C₉, C₁₂, C₁₄, C₁₅

From load combination:

P_u = 532.65 Kips = 532.65 * 1.20 = 639.18 Kips

Now,   P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g fy)

Or   639.18 = 0.80 * 0.65 * A_g (0.85 * 3.5 (1- 0.025) + 0.025 * 60)

Or    639.18 = 2.288 A_g     or   A_g = 279.36 in²  or Ag= 12” *24”

Provided Column size = 12” * 24”,   A_g   = 288 in²

 Main steel calculation:

P_u = α ф (0 .85 f′c (A_g – A_s) + A_sfy)

Or   639.18 = 0.80 * 0.65 (0.85 * 3.5 (288 – A_s) + A_s * 60)

Or   639.18 = 445.54 – 1.547 A_s + 31.20 A_s

Or   A_s = 6.53 in²     Use 4 # 8 bars + 8 # 6 bars   A_s = 6.68 in²

 Tie design:

Spacing:  S = 16 D = 16 * 6 / 8 = 12” c/c, S = 48 d = 48 * 3 / 8 = 18” c/c

At least lateral dimension: S = 12” c/c, Use # 3 bar ties @ 12” c/c.

Y – A_xis:

γ = 19 / 24 = 0.79, e_x = M_x / P = 54.898 * 12 / 532.65 = 1.24 in

e_y = M_y  / P = 1.534 * 12 / 532.65 = 0.035 in, e_x / h = 1.24 / 24 = 0.052

Reinforcement ratio:  ρ_g = A_s / A _g = 6.68 / 288 = 0.023

From Graph:  P_{n yo} / f′_c A_g = 0.98

Or P_{n yo} = 0.98 * 3.50 * 288 = 987.84 kips

P_o / f′_c A_g = 1.13 Or   P_o = 1.13 * 3.50 * 288 = 1139.04 kips

X – A_xis:  γ = 7 / 12 = 0.58, e_x = M_x / P = 54.898 * 12 / 532.65 = 1.24 in

e_y = M_y / P = 1.534 * 12 / 532.65 = 0.035 in, e_y / h = 0.035 / 12 = 0.0029

Reinforcement Ratio:  ρ_g = A_s / A _g = 6.68 / 288 = 0.023

From Graph:  P_{n xo} / f′_c A_g = 1.13

Or P_{n xo} = 1.13 * 3.50 * 288 = 1139.04 kips

P_o / f′_c A_g = 1.0   Or     P_o = 1.05 * 3.50 * 288 = 1058.40 kips

Here –   1 / P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or 1 / P_n = 1 / 1058.40 + 1 / 987.84 – 1 / 1139.04 or P_n = 926.61 kips

Now,   P_u = ф P_n   or   P_u = 0.65 * 926.61

Or    P_u = 602.30 kips > 532.65 kips, so design is ok.

Design of the Column : C₆, C₇, C₁₁, C₁₃

From load combination:

P_u = 865.56 Kips = 865.56 * 1.20 = 1038.67 Kips

Now, P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g fy)

Or   1038.67 = 0.80*0.65 * A_g (0.85 * 3.5 (1- 0.025) + 0.025 * 60)

Or   1038.67 = 2.288 A_g   or   A_g = 454 in²    or   A_g = 18” * 26”

Provided Column size = 18” * 26”,   A_g   = 468 in²

Main steel calculation:

P_u = α ф (0 .85 f’c (A_g – A_s) + A_sfy)

Or   1038.67 = 0.80 * 0.65 (0.85 * 3.5 (468 – A_s) + A_s * 60)

Or   1038.67 = 723.99– 1.547A_s + 31.20 A_s

Or    A_s = 10.61 in²    use 4 # 10 bars + 6 # 9 bars    A_s = 11.08 in²

Tie design:

Spacing:  S = 16 D = 16 * 9/8 = 18” c/c, S = 48 d = 48 * 3/8 = 18” c/c

At least lateral dimension:  S = 18” c/c,   use # 3 bar ties @ 18” c/c.

Y – A_xis:

γ = 21 / 26 = 0.80, e_x = M_x / P = 0.971 * 12 / 865.56 = 0.013 in

e_y = M_y  /  P = 61.64 * 12 / 865.56 = 0.85 in, e_x / h = 0.013 / 26 = 0.0005

Reinforcement ratio:   ρ_g = A _s  /  A _g = 11.08 / 468 = 0.024

From Graph:   P_{n yo} / f′_c A_g = 1.15

Or P_{n yo} = 1.15 * 3.50 * 468 = 1883.70 kips

P_o / f′_c A_g = 1.15   or   P_o = 1.15 * 3.50 * 468 = 1883.70 kips

X – A_xis:

γ = 13 / 18 = 0.72, e_x = M_x  /  P = 0.013 in, e_y = M_y  / P = 0.85 in

e_y / h = 0.85 / 18 = 0.047

Reinforcement ratio:  ρ_g = A_s  / A _g = 0.024

From Graph:  P_{n xo} / f′_c A_g = 1.00

Or P_{n xo} = 1.00 * 3.50 * 468 = 1638 kips

P_o / f′_cA_g = 1.15   or   P_o = 1.15 * 3.50 * 468 = 1883.70 kips

Here –   1 / P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or 1/P_n = 1 / 1638 + 1 / 1883.70 – 1 / 1883.7   or   P_n = 1638 kips

Now,   P_u = ф P_n,   or   P_u = 0.65 * 163

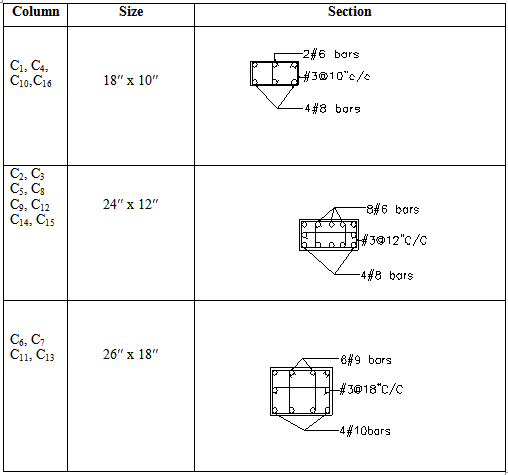
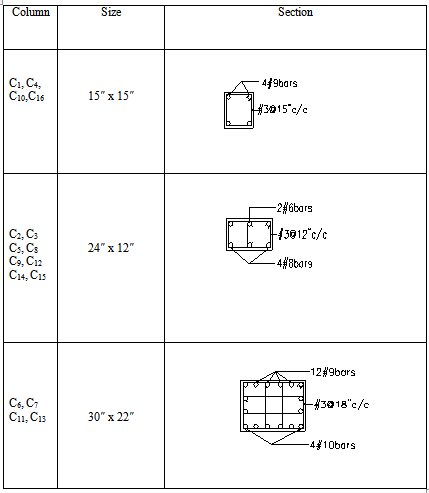
The table below is showing size of different columns of the beam supported structure.

Table 3.16: Cross -section of the Column of the beam supported structure

Column design for flat plate structure

Design of the Column : C₁, C₄, C₁₀, C₁₆

From load combination:

P_u = 232.26 Kips = 232.26 * 2.0 = 464.52 Kips

Now,    P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g f_y)

Or   464.52 = 0.80 * 0.65 * A_g (0.85 * 3.50 (1- 0.03) + 0.03 * 60)

Or   464.52 = 2.44 A_g    Or   A_g = 190.40 in².   Or   A_g = 13.79” *13.79”

Provided Column size = 15” *15”, A_g   = 225 in

 Main steel calculation:

P_u = α ф (0 .85 fc (A_g – A_s) + A_sf_y)

Or   464.52 = 0.80 * 0.65 (0.85 * 3.50 (225 – A_s) + A_s * 60)

Or   464.52 = 348.70 – 1.547A_s + 31.20  A_s.     Or     A_s = 3.92 in²

Use 4 # 9 bars,  A_s = 4.00 in²

Tie design:

Spacing: S = 16 D = 16 * 9/8 = 18” c/c, S = 48 d = 48 * 3 / 8 = 18” c/c

At least lateral dimension: S = 15” c/c, use # 3 bar ties @ 15” c/c.

Y – A_xis:

γ = 10 / 15 = 0.67, e_x = M_x / P = 94.34 * 12/232.26 = 4.87 in

e_y = M_y / P = 3.293 * 12/232.26 = 0.17 in, e_x / h = 4.87 / 15 = 0.32

Reinforcement ratio:

ρ_g = A_s / A _g = 4.00 / 225 = 0.018

From Graph,

P_{n yo} / f′_c A_g = 0.53

Or P_{n yo} = 0.53 * 3.50 * 225 = 417.37 kips, P_o/ f′c A_g = 1.09

Or     P_o = 1.09 * 3.50 * 225 = 858.37 kips

X – A_xis:

γ = 10 / 15 = 0.67, e_x = M_x / P = 4.87 in, e_y = M_y / P = 0.17 in

e_y  / h = 0.17 / 15 = 0.011

Reinforcement Ratio:    ρ_g = A_s / A _g = 0.018

From Graph:

P_{n xo} / f′_c A_g = 1.06   Or P_{n xo} = 1.06 * 3.50 * 225 = 834.75 kips

P_o / f′_c A_g =1.09       Or     P_o = 1.09 * 3.50 * 225 = 858.37 kips

Here –    1/ P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or   1/P_n = 1 / 834.75+ 1 / 417.37– 1 / 858.37     Or   P_n = 411.70 kips

Now,    P_u = ф P_n.    Or     P_u = 0.65 * 411.70

Or    P_u = 267.60 kips > 232.26 kips.       So design is ok.

Design of the Column : C₂, C₃, C₅, C₈, C₉, C₁₂, C₁₄, C₁₅

From load combination:

P_u = 469.38 Kips = 469.38 * 1.20 = 563.25 Kips

Now,    P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g f_y)

Or   563.25 = 0.80 * 0.65 * A_g (0.85 * 3.50 (1- 0.025) + 0.025 * 60)

Or   563.25 = 2.288 A_g     Or    A_g = 246.18 in²

Or   A_g =12” *24”

Provided Column size =12” *24”

A_g   = 288 in²

Main steel calculation:

P_u = α ф(0 .85 f’c (A_g – A_s) + A_sf_y)

Or   563.25 = 0.80 * 0.65 (0.85 * 3.50 (288 – A_s) + A_s * 60)

Or    563.25 = 445.54 – 1.547A_s + 31.20 A_s    Or   A_s = 3.97 in²

Use 4 # 8 bars + 2 # 6 bars,      A_s = 4.04 in²

Tie design:

Spacing:   S = 16 D = 16 * 6 / 8 = 12” c/c, S = 48 d = 48 * 3 / 8 = 18” c/c

At least lateral dimension, S = 12” c/c

Use # 3 bar ties @ 12” c/c.

Y – A_xis:

γ = 19 / 24 = 0.79, e_x = M_x / P = 94.668 * 12 / 469.38 = 2.42 in

e_y = M_y / P = 2.533 * 12 / 469.38 = 0.065 in, e_x / h = 2.42 / 24 = 0.10

Reinforcement ratio:

ρ_g = A_s / A _g = 4.04 / 288 = 0.014

From Graph:   P_{n yo} / f′c A_g = 0.86

Or P_{n yo} = 0.86 * 3.50 * 288 = 866.88 kips

P_o / f′c A_g = 1.04      Or   P_o = 1.04 * 3.50 * 288 = 1048.32 kips

X – A_xis:

γ = 7 / 12 = 0.58, e_x = M_x / P = 2.42 in, e_y = M_y / P = 0.065 in

e_y / h = 0.85 / 18 = 0.047

Reinforcement ratio:   ρ_g =A_s / A _g = 0.014

From Graph:   P_{n xo} / f′_c A_g = 1.04

Or P_{n xo} = 1.04 * 3.50 * 288 = 1048.32 kips

P_o / f′_c A_g = 1.04     Or    P_o = 1.04 * 3.50 * 288 = 1048.32 kips

Here –    1 / P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or 1 / P_n = 1 / 1048.32+ 1 / 866.88– 1 / 1048.32

Or     P_n = 869.56 kips

Now,     P_u = ф P_n.      Or     P_u = 0.65 * 869.56

Or    P_u = 565.21 kips > 469.38 kips.   So design is ok.

Design of the Column : C₆, C₇, C₁₁, C₁₃

From load combination:

P_u = 1075.60 Kips = 1075.60 * 1.40 = 1505.84 Kips

Now,     P_u = α ф A_g (0 .85 f’c (1- ρ_g) + ρ_g fy)

Or    1505.84 = 0.80 * 0.65 * A_g (0.85 * 3.50 (1- 0.03) + 0.03 * 60)

Or    1505.84 = 2.44 A_g    Or    A_g = 617.15 in  Or    A_g = 22” * 30”

Provided Column size = 22” * 30”

A_g   = 660 in²

 Main steel calculation:

P_u = α ф (0 .85 f’c (A_g – A_s) + A_sf_y)

Or    1505.84 = 0.80 * 0.65 (0.85 * 3.50 (660 – A_s) + A_s * 60)

Or    1505.84 =1021.02 – 1.547A_s + 31.20 A_s

Or    A_s = 16.35 in²

Use 4 # 10 bars + 12 # 9 bars,   A_s = 17.08 in²

Tie design:

Spacing:   S = 16 D = 16 * 9 / 8 = 18” c/c, S = 48 d = 48 * 3 / 8 = 18” c/c

At least lateral dimension,   S = 22” c/c, Use # 3 bar ties @ 18” c/c.

Y – A_xis:

γ = 25 / 30 = 0.83, e_x = M_x  /  P = 4.06 * 12 / 1075.60 = 0.045 in

e_y = M_y / P = 135.407 * 12 / 1075.60 = 1.51 in

e_x / h = 0.045 / 30 = 0.0015

Reinforcement ratio:    ρ_g = A_s / A _g = 17.08 / 660 = 0.026

From Graph:    P_{n yo} / f′c A_g = 1.108

Or P_{n yo} = 1.108 * 3.50 * 660 = 2559.48 kips

P_o / f′_c A_g = 1.20      Or    P_o = 1.20 * 3.50 * 660 = 2772 kips

X – A_xis:

γ = 17 / 22 = 0.77, e_x = M_x / P = 0.045 in, e_y = M_y / P = 1.51 in

e_y / h = 1.51 / 22 = 0.0686

Reinforcement ratio:    ρ_g = A_s  / A _g = 0.026

From Graph:   P_{n xo} / f′_c A_g = 1.09

Or P_{n xo} = 1.09 * 3.50 * 660 = 2517.90 kips

P_o/ f′_c A_g = 1.20

Or     P_o = 1.20 * 3.50 * 660 = 2772 kips

Here –     1 / P_n = 1 / P_nxo + 1 / P_nyo – 1 / P_o

Or   1 / P_n = 1 / 2517.90 + 1 / 2559.48 – 1 / 2772

Or     P_n = 2341.31kips

Now,    P_u = ф P_n.   Or     P_u = 0.65 * 2341.31

Or    P_u = 1521.85 kips > 1075.60 kips.     So design is ok.

The table below is showing size of different columns of the flat plate structure

Table 3.17: Cross section of the column elements for flat plate structure.

Some are parts:

Analysis Between a Beam Supported Structure and a Flat Plate Structure (Part 1)

Analysis Between a Beam Supported Structure and a Flat Plate Structure (Part 2)

Analysis Between a Beam Supported Structure and a Flat Plate Structure (Part 3)