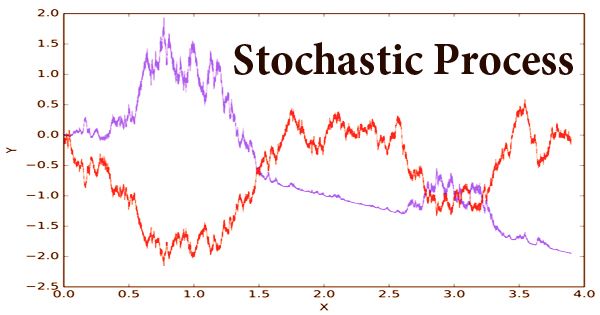
A stochastic or random process, a process involving the action of chance in the theory of probability. It is a mathematical entity that is typically known as a random variable family. Time series can be used to describe several stochastic processes. Notwithstanding, a stochastic process is commonly ceaseless while a period arrangement is a bunch of perceptions recorded by whole numbers. A stochastic cycle may include a few related arbitrary factors. For example, every atom is subject to a fixed probability of breaking down at any given time interval in radioactive decay. The growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a molecule of gas are typical examples. As mathematical models of structures and phenomena that tend to differ in a random way, stochastic processes are commonly used. They are used in many areas, such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography, and telecommunications.
Albeit stochastic process hypothesis and its applications have gained extraordinary ground as of late, there are still a ton of new and testing issues existing in the regions of hypothesis, examination, and application, which cover the fields of stochastic control, Markov chains, recharging measure, actuarial science, etc. By using more advanced theories and instruments, these problems warrant further research. In order to refer to a stochastic or random process, the term random function is often used, since a stochastic process can also be viewed as a random element in a function space. The terms stochastic process and arbitrary interaction are utilized reciprocally, regularly with no particular numerical space for the set that records the irregular factors.
A stochastic process more commonly refers to a family of random variables indexed against some other variable or variable set. It is one of the most general subjects of probability analysis. Some fundamental sorts of stochastic processes incorporate Markov measures, Poisson measures, (for example, radioactive rot), and time arrangement, with the record variable alluding to time. For example, by its state space, its index set, or the dependency among the random variables, a stochastic process can be categorized in various ways. The cardinality of the index set and the state space are one common method of classification. At the point when deciphered as time, if the file set of a stochastic interaction has a limited or countable number of components, for example, a limited arrangement of numbers, the arrangement of whole numbers, or the regular numbers, at that point the stochastic cycle is supposed to be in discrete time. If the index set is any real line interval, then time is said to be continuous.
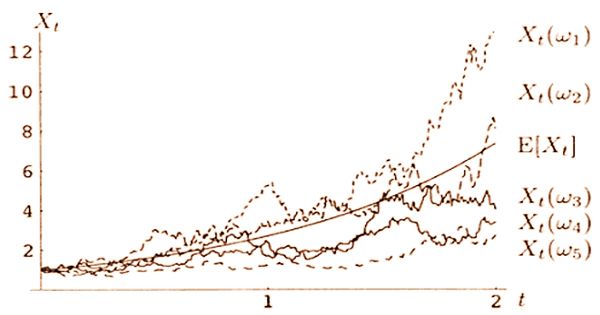
Example of Stochastic Process
The two types of stochastic processes are called stochastic processes of discrete-time and continuous-time, respectively. Discrete-time stochastic processes are considered easier to study because more advanced mathematical techniques and expertise are needed by continuous-time processes, particularly because the index set is uncountable. On the off chance that the file set is the whole numbers, or some subset of them, at that point, the stochastic process can likewise be known as an arbitrary grouping. The number of customers (X) in a checkout line is one example of a stochastic process that evolves over time. As time shifts, so do X customers, one or more at a time, come and go. If time is sampled at short intervals, X can fluctuate a little (say, one second). For longer periods, variations in X would be even larger. For example, if t is measured every hour, then the number of customers could change by tens, hundreds, or even thousands at a time.
The word stochastic in English was originally used as an adjective from a Greek word meaning “pertaining to conjecturing” with the description “to aim at a mark, guess” and the Oxford English Dictionary gives the year 1662 as its earliest occurrence. In a 1934 paper by Joseph Doob, the term stochastic process first appeared in English. The concept of a stochastic process differs, but historically a stochastic process is defined as a set of random variables indexed by some set. The terms irregular cycle and stochastic process are viewed as equivalent words and are utilized conversely, without the file set being exactly determined. Both “collection” and “family” are used, while the terms “parameter set” or “parameter space” are often used instead of “index set.”
In particular, the emphasis will be on applications of stochastic processes as key technologies in different fields of study, such as chains of Markov, renewal theory, control theory, nonlinear theory, queuing theory, risk theory, engineering of communication theory, and traffic engineering. The law of a stochastic process or an irregular variable is likewise called the likelihood law, likelihood circulation, or dissemination. With regards to the numerical development of stochastic processes, the term routineness is utilized while examining and expecting certain conditions for a stochastic process to determine conceivable development issues. For example, it is assumed that the stochastic process adheres to some sort of regularity condition, such as the sample functions being continuous, to research stochastic processes with uncountable index sets.
Information Sources: